Mediadas De Tendencia Central. Cuáles Son, Cálculo Y Representación Gráfica
La tendencia central se define como "la medida estadística que identifica un valor único como representativo de una distribución completa". Su objetivo es proporcionar una descripción precisa de todos los datos. Es el valor único que es más típico/representativo de los datos recopilados.
El término “procesamiento de números” se utiliza para ilustrar este aspecto de la descripción de datos. La media, la mediana y la moda son las tres medidas de tendencia central más utilizadas. En este artículo explicaremos cada una por separado.
¿Qué son las medidas de tendencia central?
Las medidas de tendencia central se conocen también como medidas de centro o ubicación central. Se trata de una medida de resumen que describe un conjunto completo de datos con un único valor que representa el medio o el centro de su distribución. Existen tres medidas de tendencia central que se utilizan con mayor frecuencia. Están son: la moda, la mediana y la media. Cada una de estas describe una indicación distinta del valor típico o central en la distribución.
Quizás te puede interesar: Cómo Sacar La Media Aritmética De Rendimiento Anual
¿Qué es la moda?
La moda es el valor que ocurre con mayor frecuencia en una distribución. Considera este conjunto de datos que muestra la edad de jubilación de 11 personas, en años completos: 54, 54, 54, 55, 56, 57, 57, 58, 58, 60, 60. Esta tabla muestra una distribución de frecuencia simple de los datos de la edad de jubilación.
| Envejecer | Frecuencia |
| 54 | 3 |
| 55 | 1 |
| 56 | 1 |
| 57 | 2 |
| 58 | 2 |
| 60 | 2 |
El valor más común es 54, por lo que la moda de esta distribución es 54 años.
Mira También
Cuáles Son Las Consecuencias De Respirar Por La BocaVentaja de la moda
La moda tiene una ventaja sobre la mediana y la media, ya que se puede encontrar tanto para datos numéricos como categóricos (no numéricos).
Limitaciones de la moda
Hay algunas limitaciones para usar la moda. En algunas distribuciones, la moda puede no reflejar muy bien el centro de la distribución. Cuando se ordena la distribución de la edad de jubilación de menor a mayor valor, es fácil ver que el centro de la distribución es 57 años, pero la moda es menor, 54 años.
54, 54, 54, 55, 56, 57, 57, 58, 58, 60, 60
También es posible que haya más de un modo para la misma distribución de datos (bimodal o multimodal). La presencia de más de una moda puede limitar la capacidad de la moda para describir el centro o el valor típico de la distribución porque no se puede identificar un solo valor para describir el centro.
En algunos casos, particularmente cuando los datos son continuos, la distribución puede no tener moda (es decir, si todos los valores son diferentes). En casos como estos, puede ser mejor considerar usar la mediana o la media, o agrupar los datos en intervalos apropiados y encontrar la clase modal.
¿Qué es la mediana?
Cuando hablamos de la mediana nos referimos al valor medio en la distribución cuando los valores son organizados de forma ascendente o descendente. La mediana es el valor que divide la distribución por la mitad (existe un 50 % de observaciones cada uno de los lados del valor de la mediana).
Mira También
Cómo Evitar Un CortocircuitoEn una distribución donde se presenta un número impar de observaciones, la mediana representa el valor del medio. Observando la distribución de la edad de jubilación (donde se ven 11 observaciones), la mediana representa el valor medio, que es 57 años: 54, 54, 54, 55, 56, 57, 57, 58, 58, 60, 60
Cuando en la distribución se presenta un número par de observaciones, el valor de la mediana es la media de los dos valores medios. En la distribución que se muestra a continuación, los dos valores medios son 56 y 57, entonces la mediana es 56,5 años:
52, 54, 54, 54, 55, 56, 57, 57, 58, 58, 60, 60
Ventaja de la mediana
La mediana se ve menos afectada por los valores atípicos y los datos sesgados que la media, y suele ser la medida de tendencia central preferida cuando la distribución no es simétrica.
Limitación de la mediana
La mediana no se puede identificar para datos nominales categóricos, ya que no se puede ordenar lógicamente.
¿Cuál es la media?
Cuando hablamos de la media nos referimos a la medida de tendencia central más utilizada. Hay diferentes tipos de medias; media aritmética, media ponderada, media geométrica (GM) y media armónica (HM). Si se menciona sin adjetivo (como media), generalmente se refiere a la media aritmética.
Mira También
Cómo Funciona una Secadora de CondensaciónMedia aritmética
La media aritmética (o, simplemente, "media") no es más que el promedio. Se calcula sumando todos los valores en el conjunto de datos dividido por el número de observaciones en él. Si tenemos los datos sin procesar, la media viene dada por la fórmula:
Donde, ∑ (la letra griega mayúscula sigma) se refiere a la sumatoria, X se refiere al valor individual y n es el número de observaciones en la muestra (tamaño de la muestra). Los artículos de investigación publicados en revistas no proporcionan datos sin procesar y, en tal situación, los lectores pueden calcular la media calculándola a partir de la distribución de frecuencia (si se proporciona).
Donde, f es la frecuencia y X es el punto medio del intervalo de clase y n es el número de observaciones. Se advierte a los lectores que la media calculada a partir de la distribución de frecuencias no es exactamente la misma que la calculada a partir de los datos sin procesar. Se acerca a la media calculada a partir de los datos sin procesar a medida que aumenta el número de intervalos.
Ventajas
La media utiliza todos los valores de los datos y, por lo tanto, es un buen representante de los datos. La ironía de esto es que la mayoría de las veces este valor nunca aparece en los datos sin procesar. Muestras repetidas extraídas de la misma población tienden a tener medias similares.
Mira También
Cómo Funciona Una AspiradoraLa media es por tanto la medida de tendencia central que mejor resiste la fluctuación entre distintas muestras. Está estrechamente relacionado con la desviación estándar, la medida más común de dispersión.
Desventajas
La desventaja importante de la media es que es sensible a valores extremos/valores atípicos, especialmente cuando el tamaño de la muestra es pequeño. Por lo tanto, no es una medida apropiada de tendencia central para distribución sesgada. La media no se puede calcular para datos ordinales nominales o no nominales. Aunque la media se puede calcular para datos ordinales numéricos, muchas veces no proporciona un valor significativo.
Media ponderada
La media ponderada se calcula cuando ciertos valores en un conjunto de datos son más importantes que otros. Se asigna un peso wi a cada uno de los valores xi para reflejar esta importancia.
Por ejemplo, cuando se usa la media ponderada para representar la duración promedio de la estadía de un paciente en un hospital, se toma como peso el número total de casos que se presentan en cada sala.
Media geométrica
Se define como la media aritmética de los valores tomados en una escala logarítmica. También se expresa como la raíz enésima del producto de una observación.
Mira También
5 Mejores Programas De Contabilidad Para PYMES
GM es una medida apropiada cuando los valores cambian exponencialmente y en el caso de una distribución sesgada que puede volverse simétrica mediante una transformación logarítmica. GM se usa más comúnmente en la investigación microbiológica y serológica. Una desventaja importante de GM es que no se puede utilizar si alguno de los valores es cero o negativo.
Media armónica
Es el recíproco de la media aritmética de las observaciones.
Alternativamente, el recíproco de HM es la media de los recíprocos de las observaciones individuales. HM es apropiado en situaciones donde los recíprocos de valores son más útiles. HM se usa cuando queremos determinar el tamaño de muestra promedio de varios grupos, cada uno de los cuales tiene un tamaño de muestra diferente.
Tal vez quieras conocer: Gráfico De Barras: Cómo Se Hace Manualmente Y En Excel
Mira TambiénEl Origen De La Contabilidad Y Su Evolución Histórica
Grado de variación entre las medias
Si todos los valores en un conjunto de datos son iguales, entonces las tres medias (media aritmética, GM y HM) serán idénticas. A medida que aumenta la variabilidad de los datos, también aumenta la diferencia entre estas medias. La media aritmética siempre es mayor que la GM, que a su vez siempre es mayor que la HM.
¿Qué más necesito saber sobre la media?
La media de la población se indica con el símbolo griego µ (pronunciado 'mu'). Cuando la media se calcula en una distribución de una muestra, se indica con el símbolo x̅ (pronunciado barra X).
¿Cómo influye la forma de una distribución en las medidas de tendencia central?
A continuación explicamos cómo afecta cada una de las formas de distribución en las medidas de tendencia central:
Distribuciones simétricas
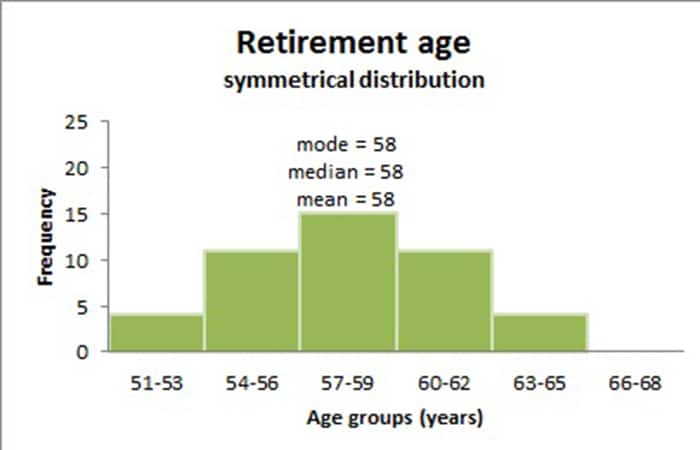
Cuando una distribución es simétrica, la moda, la mediana y la media están todas en el medio de la distribución. El siguiente gráfico muestra un conjunto de datos de edad de jubilación más grande con una distribución que es simétrica. La moda, la mediana y la media son todas iguales a 58 años.
Distribuciones asimétricas
Cuando una distribución es asimétrica, la moda sigue siendo el valor que ocurre con más frecuencia, la mediana sigue siendo el valor medio de la distribución, pero la media generalmente se "tira" en la dirección de las colas. En una distribución sesgada, la mediana suele ser una medida preferida de tendencia central, ya que la media no suele estar en el medio de la distribución.
Mira También
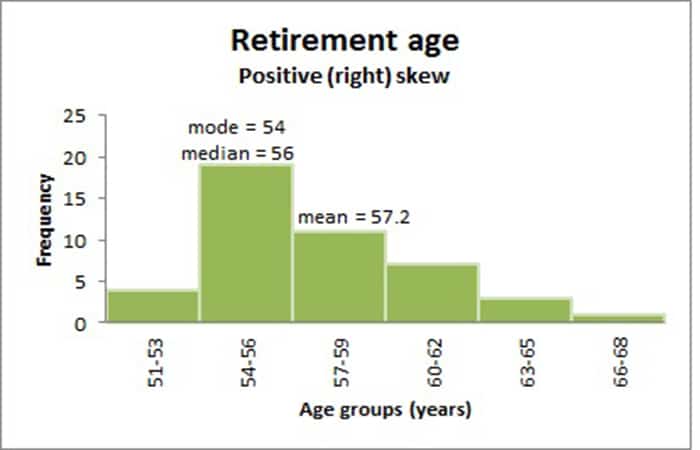
El Mejor Software De Contabilidad Para Pequeñas EmpresasSe dice que una distribución es positiva o sesgada a la derecha cuando la cola del lado derecho de la distribución es más larga que la del lado izquierdo. En una distribución con sesgo positivo, es común que la media sea 'tirada' hacia la cola derecha de la distribución. Aunque hay excepciones a esta regla, generalmente, la mayoría de los valores, incluido el valor de la mediana, tienden a ser menores que el valor medio.
El siguiente gráfico muestra un conjunto de datos de edad de jubilación más grande con una distribución asimétrica a la derecha. Los datos se han agrupado en clases, ya que la variable que se mide (edad de jubilación) es continua. La moda es 54 años, la clase modal es 54-56 años, la mediana es 56 años y la media es 57,2 años.
Se dice que una distribución es negativa o sesgada a la izquierda, cuando la cola del lado izquierdo de la distribución es más larga que la del lado derecho. En una distribución negativamente sesgada, es común que la media sea 'tirada' hacia la cola izquierda de la distribución. Aunque hay excepciones a esta regla, generalmente la mayoría de los valores, incluido el valor de la mediana, tienden a ser mayores que el valor medio.
El siguiente gráfico muestra un conjunto de datos de edad de jubilación más grande con una distribución sesgada. La moda es 65 años, la clase modal es 63-65 años, la mediana es 63 años y la media es 61,8 años.
Contabilidad Nacional. Qué Es, Significado E Importancia¿Cómo influyen los valores atípicos en las medidas de tendencia central?
Los valores atípicos son valores de datos extremos o atípicos que son notablemente diferentes del resto de los datos. Es importante detectar valores atípicos dentro de una distribución, ya que pueden alterar los resultados del análisis de datos. La media es más sensible a la existencia de valores atípicos que la mediana o la moda.
Considera nuevamente el conjunto de datos de edad de jubilación inicial, con una diferencia; la última observación de 60 años ha sido sustituida por una edad de jubilación de 81 años. Este valor es mucho más alto que los otros valores y podría considerarse un valor atípico. Sin embargo, no ha cambiado el centro de la distribución y, por lo tanto, el valor medio sigue siendo de 57 años.
54, 54, 54, 55, 56, 57, 57, 58, 58, 60, 81
Como todos los valores se incluyen en el cálculo de la media, el valor atípico influirá en el valor medio.
(54+54+54+55+56+57+57+58+58+60+81 = 644), dividido por 11 = 58,5 años
En esta distribución el valor atípico ha aumentado el valor medio. A pesar de la existencia de valores atípicos en una distribución, la media aún puede ser una medida adecuada de tendencia central, especialmente si el resto de los datos se distribuye normalmente. Si el valor atípico se confirma como un valor extremo válido, no debe eliminarse del conjunto de datos. Varias técnicas de regresión comunes pueden ayudar a reducir la influencia de los valores atípicos en el valor medio.
Preguntas frecuentes
Estas son algunas de las preguntas frecuentes que han realizado algunas de las personas interesadas en el tema. Las hemos colocado con sus respectivas respuestas:
¿Cuáles son las 4 medidas de tendencia central?
Las cuatro medidas de tendencia central son la media, la mediana, la moda y el rango medio. Aquí, el rango medio o extremo medio de un conjunto de valores de datos estadísticos es la media aritmética de los valores máximo y mínimo en un conjunto de datos.
¿Cuáles son los ejemplos de tendencia central?
La tendencia central es una estadística que representa el valor único de toda la población o un conjunto de datos. Algunos de los ejemplos importantes de tendencia central incluyen la moda, la mediana, la media aritmética y la media geométrica, entre otros.
¿Cómo encuentras la tendencia central?
La tendencia central se puede encontrar usando las fórmulas de media, mediana o moda en la mayoría de los casos. Como sabemos, la media es el promedio de un conjunto de datos dado, la mediana es el valor de datos más medio y la moda representa el valor de datos que ocurre con una frecuencia mayor en el conjunto.
¿Cuál es el propósito de la tendencia central?
El propósito de la tendencia central es proporcionar una representación exacta de todos los datos recopilados. A menudo se define como el valor único que es representativo de los datos.
¿Cuál es la diferencia entre la media y la mediana?
Cuando hablamos de la media (o media aritmética) nos referimos al promedio de todos los valores de cierto conjunto de datos. La mediana es el valor medio de los datos que se presentan.
¿Cuál es la mejor medida de tendencia central?
La media se considera la mejor medida de tendencia central a utilizar si la distribución de datos es continua y simétrica.
Echa un vistazo a: Gráfico De Líneas. Qué Es, Definición Matemática Y Creación En Excel
Pensamientos finales
La medida de tendencia central se define como el número utilizado para representar el centro o la mitad de un conjunto de valores de datos. Las tres medidas de tendencia central que se utilizan con mayor frecuencia son la media, la mediana y la moda. Una estadística que nos dice cómo se dispersan o distribuyen los valores de los datos se denomina medida de dispersión.
Una medida simple de dispersión es el rango. El rango es equivalente a la diferencia entre los valores de datos más alto y más bajo. Otra medida de dispersión es la desviación estándar, que representa la diferencia esperada (o desviación) entre un valor de datos y la media.
Deja una respuesta
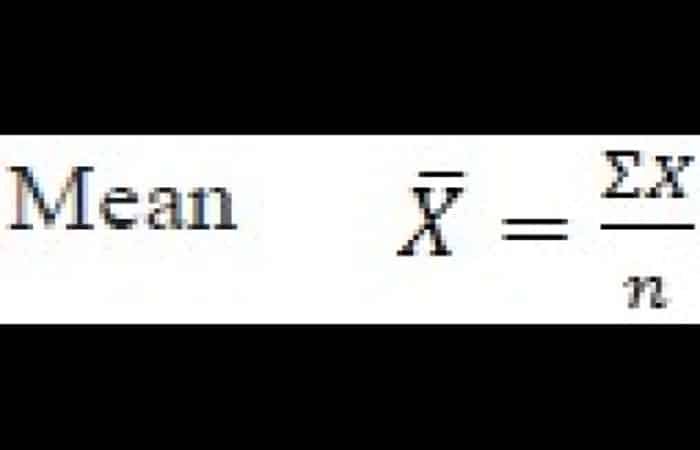
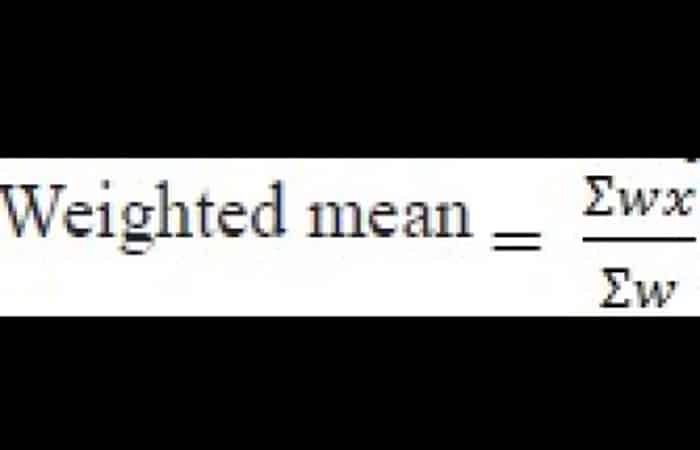
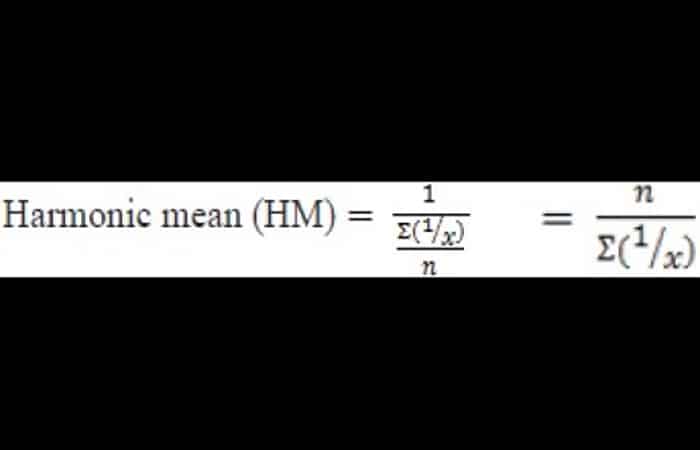
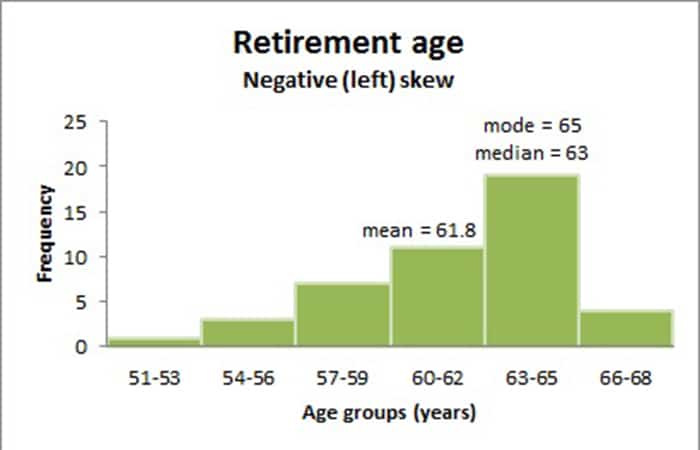
►TAMBIÉN DEBERÍAS LEER...