Cómo Sacar La Media Aritmética De Rendimiento Anual

¿Te gustaría saber cómo sacar la media aritmética de rendimiento anual de tu inversión? Aquí te enseñaremos los métodos más rápidos y precisos para obtener el resultado deseado de tus pasivos y activos. Te invitamos a quedarte con nosotros.

Cómo Calcular la media aritmética de rentabilidad anual de una inversión.

¿Cuál es el rendimiento promedio de una inversión durante 10 años? Intuitivamente tendemos a pensar que tenemos que calcular la suma de los elementos y luego dividir la suma resultante por el número de elementos, esto es lo que todos aprendimos en la escuela, esta es la media aritmética.

Aquí puedes aprender sobre: Qué Son Las Estrategias Publicitarias Y Cómo Implementarlas

Veamos qué ofrece esto para el índice Euronext 100.

Para calcular el crecimiento en porcentaje, divida el índice del año por el índice del año siguiente y reste 1, de modo que el crecimiento entre 2003 y 2004 sea (657,93 / 608,97) -1 = 0,0804 o 8,04%.

Si sumamos nuestros porcentajes y dividimos el total por el número de años, obtenemos 5.43%, que es la media aritmética de rendimiento anual. Vamos a comprobar si es correcto usando la siguiente fórmula:

Mira TambiénRequisitos para renovar un crédito Fonacot

• Valor presente = valor inicial X (1 + tasa) exponiendo el número de períodos
• 97 * (1 + 5.43%) ^ 10 = 1033.09 Lo cual no es correcto.

Es una progresión, por lo que tenemos que usar la media geométrica.

• MG = {(1 + I1) * (1 + I2) *.... * (1 + In)} ^ 1 / n
• {(1 + 0.0804) * (1 + 0.2317) *.... * (1 + 0.1896)} ^ 1/10 = 2.89%

Con Excel puedes usar la función AVERAGE.GEOMETRIC () pero con números negativos obtenemos un error. Tienes que usar factores, no porcentajes.

{= PROMEDIO.GEOMÉTRICO (1+ C4: C13) -1}

Transformamos los porcentajes en factores sumando 1 y restando 1 al final del cálculo, es un cálculo de matriz, introducimos la fórmula sin las llaves y simultáneamente presionamos las teclas CTRL + Shift + Enter para transformar la fórmula en una fórmula de matriz y las llaves se agregan automáticamente. Comprobemos que 608,97 * (1 + 2,89%) ^ 10 es de hecho igual a 809,95.

Euronext 100
2003	608,97
2004	657,93	8,04%
2005	810,35	23,17%
2006	962,84	18,82%
2007	995.23	3,36%
2008	544,92	-4 5,25%
2009	683,76	25,48%
2010	690,8	1,03%
2011	592,85	-14,18%
2012	680,87	14,85%
2013	809,95	18,96%
Promedio aritmético		5,43%	1.033,09
Significado geométrico		2,89%	809,95

Recuerda que en materia financiera cuando hablamos de promedio, es la media geométrica.

Mira TambiénRequisitos para Crédito Fonacot por primera vez

Ejemplo de media geométrica y media aritmética de rendimiento anual

Una compañía te ofrece una gran oferta: si compras acciones de XYZ hoy, la compañía te garantiza los siguientes rendimientos:

• + 50% la primera semana y -40% la segunda.

No está mal, no, una ganancia media.5% por semana ¡No es una mala estafa especialmente! Efectivamente, en este ejemplo, si colocas 1000 euros en la empresa XYZ, tu inversión tendrás al final de la 1a semana un valor total de 1500 euros (1000 euros * (1 + 50%))

Pero al final de la segunda semana, tu cartera tendrá un valor total de solo 900 euros (1500 euros * (1 - 40%)), que es menor que su valor original.

Ejemplo del mal uso de la media aritmética de rendimiento anual

Aquí hay un ejemplo simple que muestra por qué definitivamente no debes usar la media aritmética (suma de rendimientos dividida por el número de períodos) cuando quieres ver el desempeño de una cartera durante varios períodos. Pero entonces, ¿qué deberías usar?

De hecho, es bastante simple. En este ejemplo a continuación, el primer año el valor de tu cartera se multiplicó por 1,5 (1 + 50% = 1,5) y el segundo año por 0,6 (1 - 40% = 0,6).

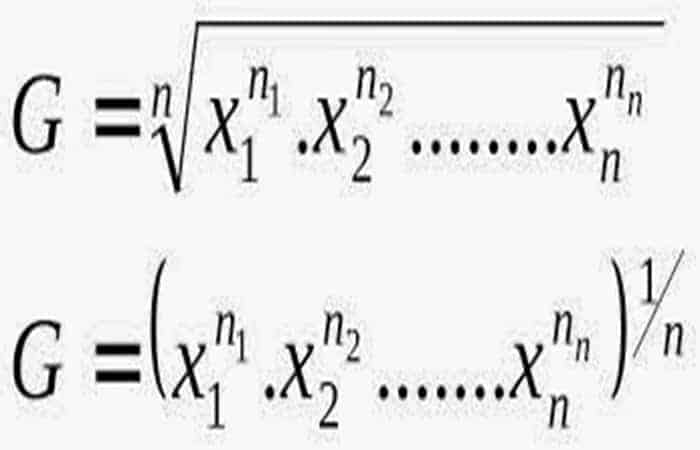
Para calcular la media aritmética de rentabilidad anual, la fórmula a utilizar es la denominada media geométrica, que es igual a la raíz enésima (siendo n el número de periodos) de la multiplicación de las rentabilidades, de las que restamos 1. Sigue estos pasos:

Mira TambiénCómo Saber si Tengo DICOM

• Paso 1: En este ejemplo, tenemos (1) n = 2 (dos períodos) y (2) una cartera multiplicada por 1,5 en el primer período y luego multiplicada por 0,6 en el segundo.
• Paso 2: Luego multiplicas 1,5 por 0,6, lo que da 0,9
• Paso 3: Luego, tomas la raíz cuadrada (debido a dos períodos) de 9 (= 0.948) de la cual restas 1 ----> y aquí está tu rendimiento promedio por período de -5.2%.

Al aplicar esta rentabilidad media por periodo, significa suavizando las rentabilidades que al final de la 1a semana tu cartera tendrá un valor de 1000 * (1 - 5,2%) = 948,7 euros, y al final por segundo de 948,7 euros. * (1 - 5,2%) = 900 euros.

Luego encontramos nuestros "900 euros" de la introducción, pero en lugar de un rendimiento por período calculado mediante la media aritmética de + 5% (50% - 40% dividido por 2), el rendimiento real, calculado mediante la media geométrica es - 5,2%. Todavía hace una pequeña diferencia.

Ejemplo 2 mal uso de la media aritmética de rendimiento anual

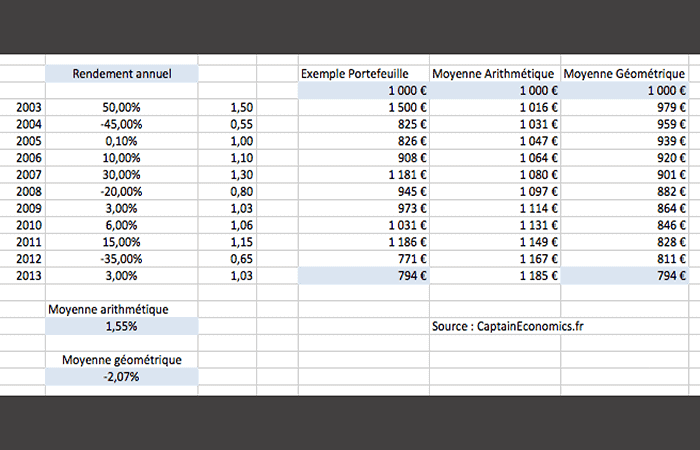
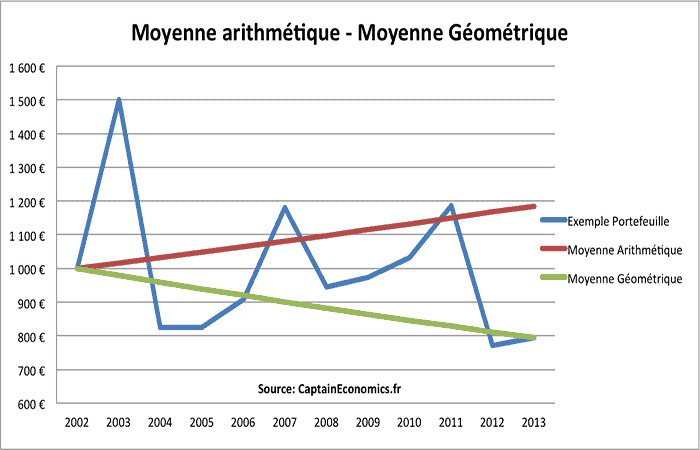
Tomemos un segundo ejemplo rápido. Supongamos que se te proporciona la siguiente tabla, con el rendimiento anual de una cartera entre 2003 y 2013.

En 2003, tu cartera ganó un 50%, luego perdió un 45% en 2004, etc. Consideramos la media aritmética de rendimiento anual (Media “clásica”), por tanto llegamos a + 1,55% anual.

Siguiendo la media aritmética, 1000 euros invertidos en 2003 valdrían finalmente 1185 euros.

Pero en realidad, si aplicamos las variaciones de esta cartera considerando la evolución año a año de una inversión inicial de 1000 euros, nos damos cuenta de que a finales de 2013, tu cartera solo vale 794 euros.

Mira TambiénCómo Solicitar Un Crédito Fonacot para Damnificados

Y obviamente llegamos a la misma cifra calculando la media geométrica, con una rentabilidad media anual de -2,07%.

En Excel, puedes simplemente calcular la media geométrica a través de la función "PROMEDIO.GEOMÉTRICO ()" o "GEOMÉTRICO ()". Para calcularlo a mano, aquí está la fórmula:

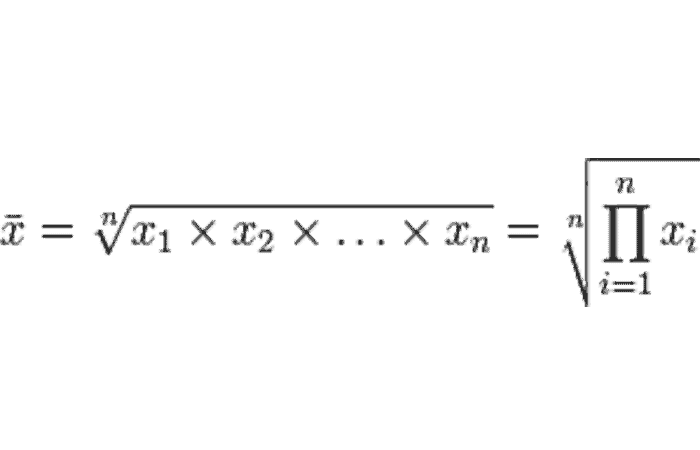
• Para evitar el problema en caso de valor negativo, debes considerar las variables "x" como el valor de la multiplicación a través del rendimiento; por ejemplo, un rendimiento de + 20% corresponde a un valor de 1,20.
• Luego, solo necesitas restar 1 de la fórmula a continuación para encontrar el rendimiento promedio por período de tu cartera.

NOTA: Nunca tomes la media aritmética de rendimiento anual para un cálculo con tasas de cambio durante varios períodos (lo mismo para el crecimiento promedio del PIB, la tasa promedio de inflación durante x períodos) A menos que seas SM y te guste ser pateado por las reglas.

¿Cómo calcular la rentabilidad anual de tu cartera?

Después de haber discutido extensamente los 3 casos teóricos de la parte anterior, no se debe concluir especialmente que no se pueden calcular tus propios rendimientos.

Por supuesto, hay que seguir pensando que no deberíamos correr tras una cifra exacta, pero dado que invertimos de forma pasiva, sin transacciones excesivas, deberíamos poder medir un escenario realista contra el rendimiento mostrado en sitios especializados.

Mira TambiénCómo Transferir Dinero Desde Una Tarjeta De Crédito A Otra En Línea

Entonces hay que medir el desempeño de una cartera canadiense invertida en ZCN para tomarlo como ejemplo.

Este fondo incluye más de 200 acciones de empresas canadienses y captura el rendimiento del 95% del mercado de valores canadiense (según el sitio de todos modos).

En este ejemplo nuestro inversor se llamará (INVERSOR) y comienza en 2015 hasta 2020 invirtiendo $ 2,000 cada mes.

Comienza el cálculo de media aritmética de rendimiento anual

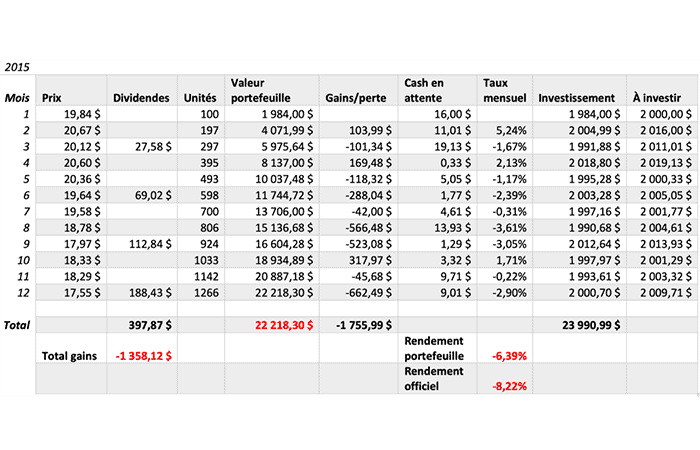
El mercado de valores canadiense no vivió bien con la caída de los precios del petróleo en 2015. El impacto que esto ha tenido en esta provincia en lo que va de 2021 se ha prolongado.

Pero lo más importante aquí es el rendimiento de la cartera en -6,39%, muy lejos del rendimiento oficial del -8,22%, por ejemplo.

Mira TambiénDerivado De Crédito – Ejemplos y Tipos

Hay que tenga en cuenta que se incluyen dividendos que se reinvierten. Este es realmente el rendimiento total bruto. Aquí se buscarán los precios de los fondos de ZCN mes a mes, así como los montos de dividendos.

Para los propios cálculos, todo lo que tienes que hacer es conectarte a tu sitio de corretaje en línea, encontrar los detalles de tus transacciones e ingresar los datos correctos, como la cantidad de inversiones netas después de los costos de transacción, la cantidad de dividendos netos, etc.

La tabla está en bruto, pero debes calcular tu red. En este ejemplo, a pesar de las contribuciones mensuales desiguales (entre $ 1.984 y $ 2.018), todavía es posible calcular un promedio que se acerque a nuestro ETF.

El objetivo entonces será acercarse lo más posible a la tasa bruta reduciendo los costos y optimizando los impuestos.

Ahora veamos más detalles sobre los cálculos. Pasemos al 2016:

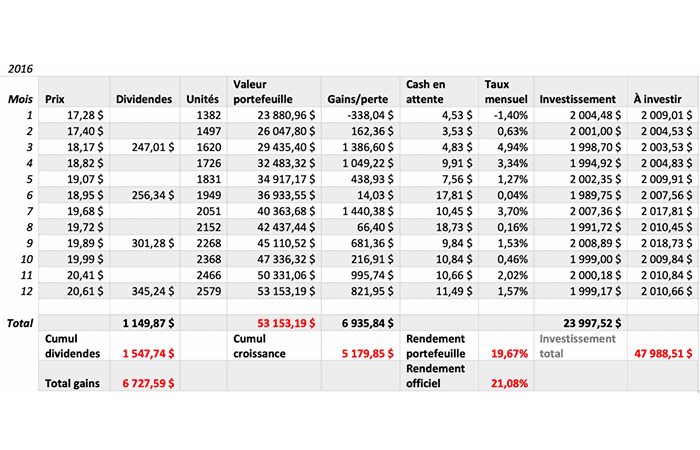
• En 2016 el mercado repuntó… Pero lo único que queremos es ver el 19,67%de nuestra cartera frente al 21,08% del ETF.

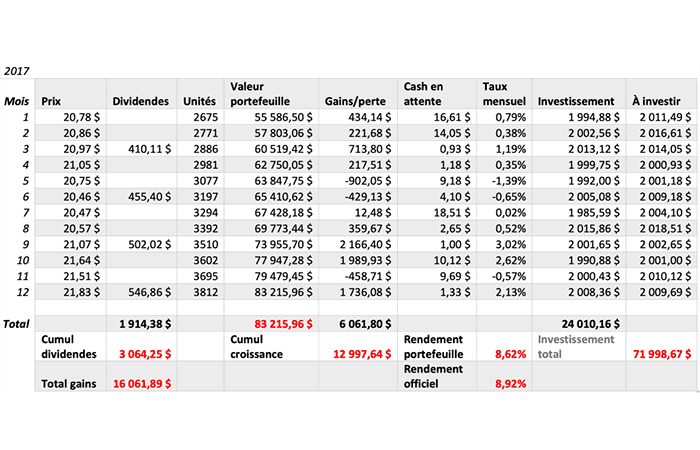
• En 2017, los mercados canadienses acogieron con satisfacción la noticia de la elección de Emmanuel Macron en Francia... Mientras tanto, aquí está el 8,62%para nuestra cartera frente al 8,92% para el ETF.

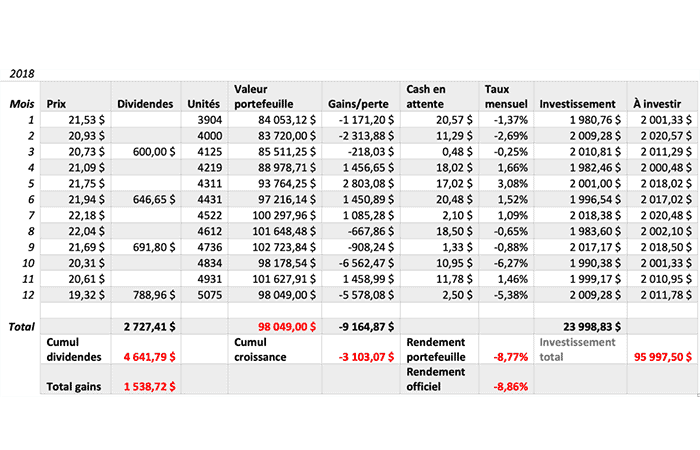
• En 2018 Rusia, Kazajstán, Azerbaiyán, Irán y Turkmenistán firman la convención sobre el estado del Mar Caspio y, sorprendentemente, los mercados canadienses no parecen apreciarse. Aquí la media aritmética de rendimiento anual es aproximadamente: -8,77%contra -8,86%.

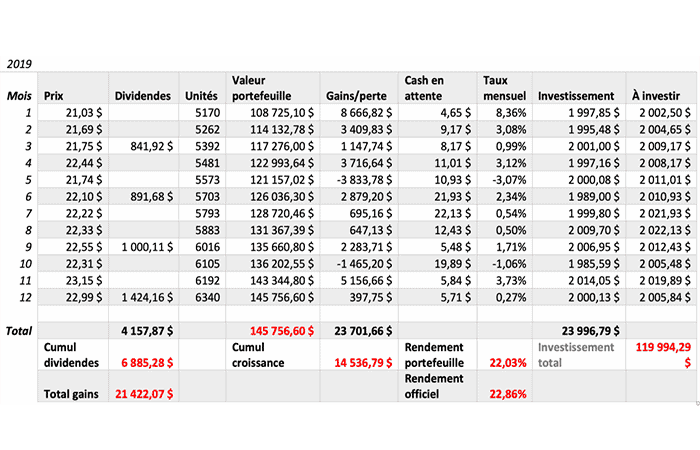
• En 2019, las revistas People y Vanity Fair eligieron a Celine Dion como la personalidad mejor vestida del año. Los inversores canadienses conocedores aumentaron la cartera un 22,03% a un 22,86%.

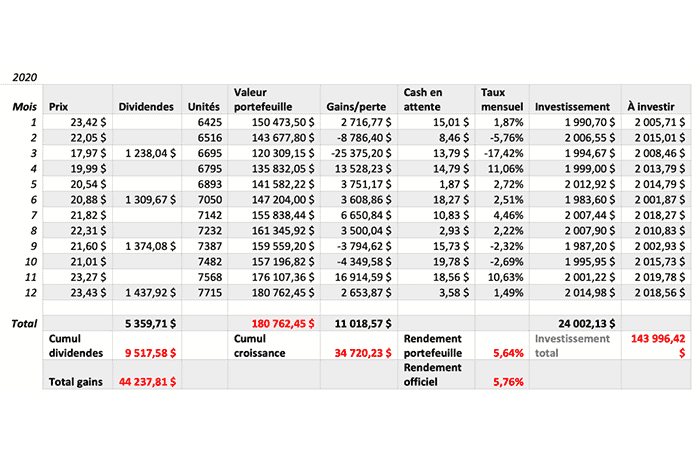
Todo el mundo sabe que 2020 estuvo marcado por la aparición de una ballena cerca de Montreal en el río San Lorenzo. Esto vale un 5,64% frente a un 5,76%.

Mira TambiénCómo Transferir Dinero Desde Una Tarjeta De Crédito A Otra

Revisión de 6 años de la media aritmética de rendimiento anual

(EL INVERSOR) tiene una cartera de acciones de $ 180.762,45. Invirtió de su propio bolsillo un total de $ 143.996,42 lo que le reportó una ganancia de capital de $ 34.720,23 y dividendos reinvertidos de $ 9.517,58 para una ganancia total de $ 44.237,81.

Debes tener en cuenta que los dividendos representan más del 21% de la ganancia total. Sería una pena descuidarlos como hacen la mayoría de los gráficos estándar.

• Por ejemplo: Tenía 2 años negativos en -6 y -8% aproximadamente y 2 años entre 19 y 20%. Para la anécdota, hay que mirar los meses de febrero y marzo de 2020 donde pierde $ 34,000 en 2 meses. La ganancia de casi $ 17.000 en noviembre corresponde al anuncio de la vacuna.

Solo queda ahondar en los cálculos en detalle y también encontrar la tasa anual que ha tenido durante estos 6 años. Sigamos al siguiente paso:

Tasa de rendimiento ponderada en el tiempo

Otro nombre para dormir al aire libre pero tiene similitudes con la media geométrica. Esta tasa permite cancelar el efecto de las contribuciones mensuales para centrarse únicamente en las ganancias. Para hacer esto, necesitas conocer la ganancia mensual:

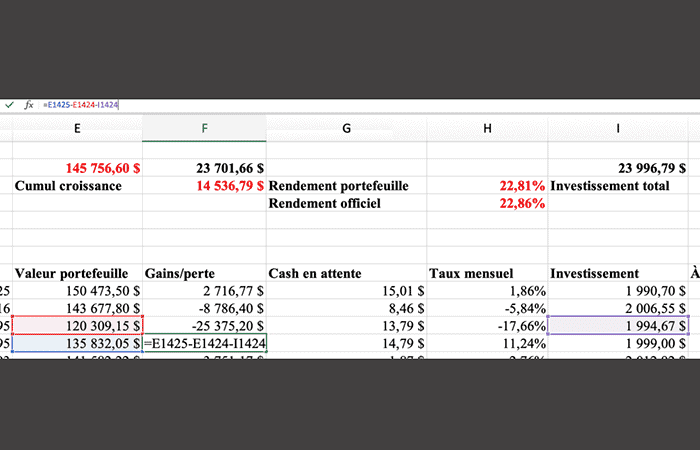
Aquí debes utilizar estas formula: Ganancia mensual = valor final - valor inicial - monto neto invertido.

• En la imagen de arriba, el valor final está en azul 135,832.05.
• El valor final está en rojo 120,309.15
• y el monto invertido está en morado 1,994.67.

Este último no es 2000 porque solo puedes comprar unidades enteras. Como resultado, siempre hay un “desperdicio” de liquidez que permanece pendiente en la cuenta.

Mira TambiénRiesgo De Crédito. Qué Es, Cómo Se Calcula Y Tipos

El mes siguiente debes intentar invertir este desperdicio pero habrá 1 más, etc. No incluyas dividendos cuando calcules el monto invertido. De hecho, aunque reinviertes los dividendos, los genera tu inversión y no tu directamente.

Si los incluye en tu contribución, es como no contarlos como un factor de retorno (sería una pena).

Calculo de media aritmética de rendimiento anual (tarifa mensual)

Ahora puedes calcular tu tarifa mensual:

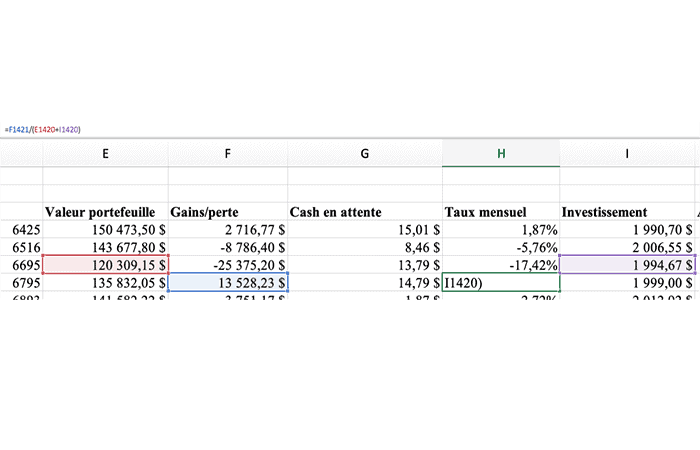
Debes utilizar esta fórmula: Tasa mensual = ganancia mensual / (valor inicial + contribución anterior)

• El valor inicial está en rojo y la ganancia en azul.
• La contribución anterior está en violeta.

Para expresarlo como un porcentaje lo multiplica por 100 o simplemente haces clic en el botón de porcentaje en Excel. Si realizaste un retiro y no una contribución, debes restar la última inversión en lugar de sumarla.

Ahora que tienes tu tasa mensual, todo lo que tienes que hacer es calcular la famosa Tasa de rendimiento ponderada en el tiempo para el año (TRPT):

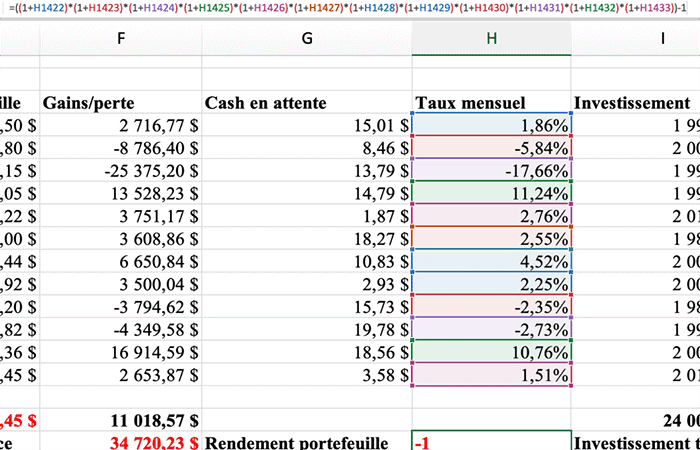
Debes utilizar esta fórmula: TRPT = [(tasa 1 + mes 1) (tasa 1 + mes 2)… (Tasa 1 + mes 12)] - 1

La fórmula en la parte superior de la imagen debería dejarlo todo claro.

Cálculo de la Tasa anual invertida

A continuación, te indicamos cómo encontrar la tasa anual si inviertes una vez al mes. Si tienes 30 movimientos de liquidez por mes, se necesitarán 30 líneas de cálculo por mes y 360 tasas que se multiplicarán al final.

Esta tasa te permite comparar la cartera con un índice pero existe otra tasa que resaltará mejor los momentos en los que ha realizado tus compras o ventas.

• Básicamente, te dirá si hubiera sido mejor ir a pescar en lugar de invertir ese día.

2 velocidades diferentes para expresar el mismo resultado. Como dijimos anteriormente, estas son 2 fotografías tomadas desde diferentes ángulos. No existe un número absoluto, pero la TRPT tiene la ventaja de ser más fácil de calcular que la 2ª tasa, que también se denomina: tasa de retorno ponderada según el valor monetario (TRPM). Para la inversión pasiva, el TRPT es en gran medida suficiente.

Entonces, ¿qué pasa con el promedio anualizado de nuestros 6 años de inversión? El número mágico es solo un promedio geométrico de nuestros 6 TRPT:

[(1 + (- 8,29%)) (1 + 20,9%) (1 + 8,88%) (1 + (- 8,94%)) (1 + 22,81%) (1+ 5,66%)] ^ (1/6) -1 = 6,16% anual. No es suficiente para clamar por una burbuja financiera... al menos en Canadá.

Excel tiene una fórmula para la media geométrica, pero si expresaste tu TRPT como un porcentaje, deberá manipularlo ligeramente:

• Paso 1: Debes agregar 1+ antes de seleccionar celdas y hacer -1 al final.
• Paso 2: Luego, debes validar todo como una fórmula matricial haciendo shift + ctrl + Enter.

Además, solo se hace esto para un fondo. Deberías agrupar todos los ETF en los que inviertes para encontrar las ganancias totales y los montos invertidos antes de calcular cada tasa mensual para toda la cartera.

Si quieres ver cuánto puedes elegir las fechas en las que quieres mostrar las rentabilidades que te convengan, quita 2015 del cálculo y tendrás un 8,86% anual para tu cartera en lugar de un 6,16.

Las finanzas muestran un 8.30% para ZCN durante los últimos 5 años, ¡así que supera al ETF! ¡Ya es hora de que inicies tu propio fondo de cobertura!

Con tal desempeño, si tu futuro fondo de cobertura solo cobra un 0,6% en comisiones, perderías la ventaja frente al ETF.

¿Realmente tenemos que hacer todo esto para la media aritmética de rendimiento anual?

¡No! Experimenta haciendo estos mismos cálculos al no incluir la inversión anterior en la división de tarifas mensuales y te dará una tasa anual de 6,10% en lugar de 6,16%.

Por otro lado, los primeros 2 años, están mucho más cerca del desempeño de la ETF. Así que todos los meses durante 6 años cometo un pequeño error de cálculo y solo tienes una desviación de 6 puntos básicos del resultado real.

• No decimos que debes cometer errores de cálculo, pero es inútil buscar una precisión absoluta.

Cuanto más activamente invierta en muchas transacciones o grandes movimientos de efectivo durante el año, menos te será útil el TRPT y más correrás el riesgo de cometer errores en tus cálculos.

Es muy fácil cometer errores y copiarlos y pegarlos año tras año y quedarse dormido con la certeza de un buen rendimiento.

• Por ejemplo: Brad Barber y Terrance Odean estudiaron 66.465 cuentas individuales entre 1991 y 1996. Aquellos que eran más activos en sus cuentas arrojaron un 11,4% frente al 17,9% del índice. Si estos inversores activos hubieran medido correctamente su desempeño, podrían haber entendido que no valía la pena insistir.

También te puede interesar leer sobre: ¿Cómo Obtener Crédito Si Tengo DICOM?

Conclusión

Si inviertes pasivamente, debes tomar los números que muestran sus ETF en Internet y asume que lo estás haciendo un poco peor, especialmente después de las comisiones y los impuestos.

Cuando pagues tu préstamo hipotecario, espera que todos los meses no calcules tu TRPT basándote en algún tipo de estimación del valor de tu casa. El monedero es transparente y es muy conveniente. Pero, honestamente hablando, no hay tiempo para dedicar tu tiempo a hacer todos estos cálculos a menos que estés interesado en el lado puramente teórico.

Si es así, bienvenido al club, si no, no te engañes con misiones para optimizar tu tasa y estrategias de sincronización del mercado para aumentar tu rendimiento en unos pocos puntos básicos. Concéntrate en ahorrar más y reducir tus costos e impuestos, tendrás mucho más impacto. Esperamos haberte ayudado a entender un poco mejor cómo sacar la media aritmética de rendimiento anual.