Cómo Encontrar El Mínimo Y El Máximo De Una Función
Encontrar el mínimo y el máximo de una función puede resultar muy útil. A menudo surge en problemas de optimización que no tienen restricciones, o en los que las restricciones no impiden que la función alcance su mínimo o máximo.
Este tipo de problemas ocurren mucho en la práctica. Un ejemplo sería determinar el precio de un determinado artículo. Si conoces la demanda de un precio determinado (o una buena estimación de la demanda), puedes calcular el precio por el que obtendrás el mayor beneficio. Esto se puede formular como hallar el máximo de la función de beneficio.
El mínimo y el máximo de una función también se denominan puntos extremos o valores extremos de la función. Pueden ser locales o globales.
Quizás te puede interesar: Cómo Calcular Porcentajes Promedio - Guía
El mínimo y el máximo de una función: Extrema local y global
Un mínimo / máximo local es un punto en el que la función alcanza su valor más bajo / más alto en una determinada región de la función. En palabras formales, esto significa que para cada mínimo / máximo local x, hay una épsilon tal que f (x) es menor / mayor que todos los valores f (y) para todas las y que tienen una distancia máxima de épsilon ax.
Eso parece muy complicado, pero significa que f (x) es el valor más pequeño / más grande para todos los puntos cercanos a x. Sin embargo, puede haber valores que sean más pequeños / más grandes que el mínimo / máximo local, pero están más lejos.
Mira También 5 Tipos De Contratos Comerciales Y Ejemplos
5 Tipos De Contratos Comerciales Y EjemplosEl mínimo global es el valor más pequeño que toma la función en todo su dominio. De manera equivalente, el máximo local es el valor más grande de la función. Por lo tanto, cada punto extremo global es también un punto extremo local, pero lo contrario no es cierto.
¿Todas las funciones tienen un mínimo y un máximo?
Una función no tiene necesariamente un mínimo o un máximo. Por ejemplo, la función f (x) = x no tiene mínimo ni máximo. Esto se puede ver fácilmente de la siguiente manera. Supón que la función tiene un mínimo en x = y. Luego completa y-1 y la función tendrá un valor menor. Por tanto, tenemos una contradicción y “y” no era el mínimo y, por tanto, el mínimo no existe. Se puede dar una prueba equivalente para el máximo.
La función f (x) = x2 tiene un mínimo, es decir, en x = 0. Esto se verifica fácilmente ya que f (x) nunca puede volverse negativo, ya que es un cuadrado. En x = 0, la función tiene valor 0, por lo que debe ser el mínimo. No tiene un máximo, que se puede probar usando exactamente el mismo argumento que usamos antes.
Cómo encontrar los puntos extremos de una función
En un mínimo local, la función cambia de dirección. Esto se debe a que es el punto más bajo. Por lo tanto la pendiente de la función va de negativa a positiva, ya que la función fue decreciendo hasta llegar al mínimo y luego comenzó a aumentar nuevamente.
Esto significa que en el mínimo local, la pendiente es igual a cero y, por lo tanto, la derivada de la función debe ser igual a cero en el punto que es el mínimo. Lo mismo ocurre con el máximo local de una función, ya que allí la función pasa de aumentar a disminuir.
Por lo tanto, para encontrar la ubicación de los máximos y mínimos locales, debes resolver la ecuación f '(x) = 0. Por lo tanto, primero debes encontrar la derivada de la función. Si no estás familiarizado con la derivada, o si te gustaría saber más sobre ella, te recomendamos estudiar sobre esto. Para este artículo suponemos que se conoce la derivada.
Mira También Cómo Detectar Monedas De Oro Y Plata Falsas. 8 métodos
Cómo Detectar Monedas De Oro Y Plata Falsas. 8 métodosDespués de haber resuelto la ecuación f (x) = 0, habrás encontrado las ubicaciones en las que se encuentran los extremos. Para encontrar el valor de los extremos, debes completar la ubicación en la función. De las soluciones no se puede ver directamente si es un mínimo local o un máximo local, ya que ambos son soluciones de la misma ecuación. Por lo tanto, debes trazar la función para determinar esto.
Además, no puedes decir directamente si has encontrado un mínimo o máximo global, o si es solo local. Además, puedes determinar esto con la ayuda de la gráfica de la función.
Tal vez quieras conocer: ¿Cómo Saber Si Un Número Es Primo?
Ejemplos
Aquí tienes algunos ejemplos sencillos de máximos y mínimos de una función:
Ejemplo 1
Sea f (x) = x 2 - 6 x + 5.
¿Existen valores críticos, algún punto de inflexión? Si es así, ¿determinan un máximo o un mínimo? ¿Y cuáles son las coordenadas en el gráfico de ese máximo o mínimo?
Mira También Estructura Organizativa Matricial. Guía Completa
Estructura Organizativa Matricial. Guía CompletaSolución
f' ( x ) = 2 x - 6 = 0 implica x = 3.
x = 3 es el único valor crítico. Es la coordenada x del punto de inflexión. Para determinar la coordenada y, evalúa f en ese valor crítico; evalúa f(3):
f(x) = x2 - 6 x + 5
f (3) = 32 − 6• 3 + 5 = −4.
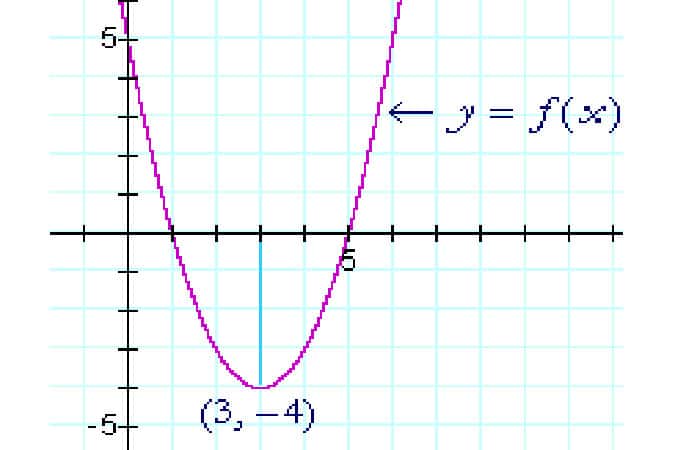
El valor extremo es −4. Para ver si es un máximo o un mínimo, en este caso simplemente podemos mirar el gráfico.
 Organizaciones Sin Fines De Lucro (Definición Y Ejemplos)
Organizaciones Sin Fines De Lucro (Definición Y Ejemplos)F (x) es una parábola y podemos ver que el punto de inflexión es mínimo. Al encontrar el valor de x donde la derivada es 0, hemos descubierto que el vértice de la parábola está en (3, −4).
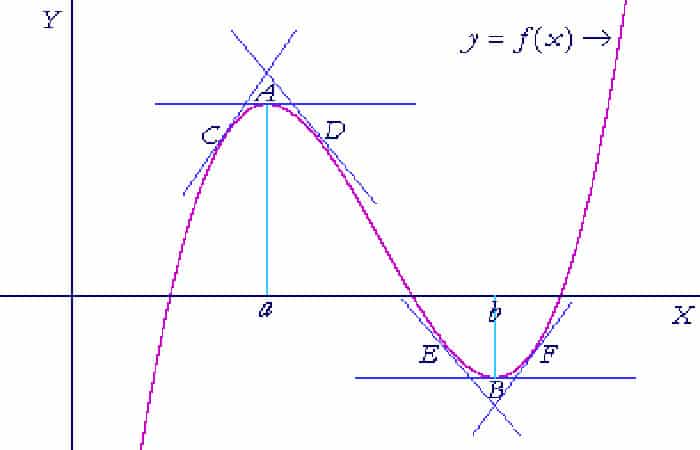
Pero no siempre podremos mirar el gráfico. La condición algebraica para un mínimo es que f ' (x) cambia de signo de - a +. Vemos esto en los puntos E, B, F anteriores. El valor de la pendiente aumenta.
Ahora, decir que la pendiente está aumentando es decir que, en un valor crítico, la segunda derivada, que es la tasa de cambio de la pendiente, es positiva. Nuevamente, aquí está f (x):
f (x) = x 2 - 6 x + 5.
f' (x) = 2 x - 6.
f'' (x) = 2.
Mira También Gráfico Circular O Gráfico De Pastel. Qué Es, Usos Y Alternativas
Gráfico Circular O Gráfico De Pastel. Qué Es, Usos Y Alternativasf'' evaluado en el valor crítico 3 - f'' (3) = 2 es positivo. Esto nos dice algebraicamente que el valor crítico 3 determina un mínimo.
Condiciones suficientes
Ahora podemos establecer estas condiciones suficientes para valores extremos de una función en un valor crítico a:
La función tiene un valor mínimo en x = a si f '(a) = 0 y f'' (a) = un número positivo. La función tiene un valor máximo en x = a si f' (a) = 0 y f'' (a) = un número negativo. En el caso del máximo, la pendiente de la tangente es decreciente; va de positivo a negativo. Podemos ver que en los puntos C, A, D.
Ejemplo 2
Sea f (x) = 2 x 3 - 9 x 2 + 12 x - 3.
¿Existen valores extremos? Primero, ¿existen valores críticos - soluciones de f' (x) = 0 - y determinan un máximo o un mínimo? ¿Y cuáles son las coordenadas en el gráfico de ese máximo o mínimo? ¿Dónde están los puntos de inflexión?
Mira También Teorema Del Límite Central: Definición Y Ejemplos
Teorema Del Límite Central: Definición Y EjemplosSolución
f' ( x ) = 6 x 2 - 18 x + 12 = 6 ( x 2 - 3 x + 2) = 6 ( x - 1) ( x - 2) = 0
implica: x = 1 o x = 2.
Esos son los valores críticos. ¿Cada uno determina un máximo o determina un mínimo? Para responder, debemos evaluar la segunda derivada en cada valor.
f' (x) = 6 x 2 - 18 x + 12.
f'' ( x ) = 12 x - 18.
f'' (1) = 12 − 18 = −6.
Mira También Método De Newton Raphson. Cálculo Y Ejercicios Resueltos
Método De Newton Raphson. Cálculo Y Ejercicios ResueltosLa segunda derivada es negativa. Por tanto, la función tiene un máximo en x = 1. Para encontrar la coordenada y, el valor extremo, en ese máximo, evaluamos f (1):
f (x) = 2 x 3 - 9 x 2 + 12 x - 3
f (1) = 2 − 9 + 12 – 3 = 2.
El máximo ocurre en el punto (1, 2).
A continuación, ¿determina x = 2 un máximo o un mínimo?
f'' ( x ) = 12 x - 18.
f'' (2) = 24 − 18 = 6.
La segunda derivada es positiva. Por tanto, la función tiene un mínimo en x = 2.
Para encontrar la coordenada y - el valor extremo - en ese mínimo, evaluamos f (2):
f (x) = 2 x 3 - 9 x 2 + 12 x - 3.
f (2) = 16 − 36 + 24 – 3 = 1.
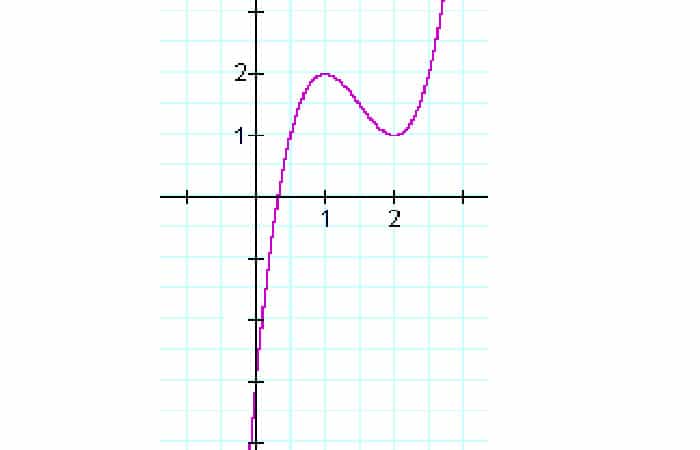
El mínimo ocurre en el punto (2, 1). Aquí, de hecho, está la gráfica de f (x):
Las soluciones de f'' (x) = 0 indican un punto de inflexión en esas soluciones, no un máximo ni un mínimo. Un ejemplo es y = x3. y'' = 6 x = 0 implica x = 0. Pero x = 0 es un punto de inflexión en la gráfica de y = x 3, no un máximo ni un mínimo.
Otro ejemplo es y = sin x. Las soluciones de y'' = 0 son las multiplicaciones de π, que son puntos de inflexión.
Pensamientos finales
El mínimo y el máximo de una función se llaman puntos extremos. Un punto extremo local es el valor más pequeño o más grande en el conjunto de valores. Si también es el más pequeño o el más grande en todo el dominio de la función, se denomina punto extremo global.
Echa un vistazo a: Ley De Distribución Normal – Qué Es Y Cómo Utilizarla
Los mínimos y máximos locales se pueden encontrar resolviendo f'(x) = 0. Luego, utilizando la gráfica de la función, puedes determinar si los puntos que encuentras eran un mínimo local o un máximo local. Además, puedes determinar qué puntos son los extremos globales.
No todas las funciones tienen un mínimo / máximo (local). E incluso si una función tiene un mínimo local, puede suceder que no exista un mínimo global. Lo mismo vale para el máximo. Además, el mínimo y el máximo globales no tienen por qué ser únicos. Puede suceder que en varios puntos la función alcance su valor más pequeño o más grande.
Deja una respuesta

►TAMBIÉN DEBERÍAS LEER...