Método De Newton Raphson. Cálculo Y Ejercicios Resueltos
El método de Newton-Raphson es una técnica poderosa para resolver ecuaciones numéricamente. Utiliza la idea de que una función continua y diferenciable puede aproximarse mediante una línea recta tangente a ella.
La idea comienza con una suposición inicial que está razonablemente cerca de la raíz verdadera, luego para aproximar la función por su línea tangente y para calcular la intersección con el eje x de esta línea tangente por álgebra elemental.
Esta intersección con x será típicamente una mejor aproximación a la raíz de la función original que la primera aproximación, y el método se puede iterar.
Quizás te puede interesar: 10 Mejores Páginas Webs Para Resolver Problemas Matemáticos
Mira TambiénCómo Llenar El Libro Mayor De Contabilidad
Cómo funciona el método de Newton Raphson
Supón que necesitas encontrar la raíz de una función diferenciable continua f (x)f ( x )y sabes que la raíz que estás buscando está cerca del punto x = x_0x=x0. Entonces el método de Newton nos dice que una mejor aproximación para la raíz es:
Este proceso puede repetirse tantas veces como sea necesario para obtener la precisión deseada. En general, para cualquier x-valor x_nxnorte, el siguiente valor viene dado por:
Nota: el término "cerca" se usa de manera vaga porque no necesita una definición precisa en este contexto. Sin embargo, x_0x0 debe estar más cerca de la raíz que necesita que de cualquier otra raíz (si la función tiene varias raíces).
La base de la formulación
El método de Newton-Raphson es un algoritmo de búsqueda de raíces que utiliza los primeros términos de la serie de Taylor de una función. Para resolver la ecuación f (x) = 0, se considera la primera expansión de Taylor de la función f (x),
Mira También Matraz Volumétrico - ¿Qué Es, Cómo Funciona Y Para Qué Sirve?
Matraz Volumétrico - ¿Qué Es, Cómo Funciona Y Para Qué Sirve?Si f (x) es lineal, solo los dos primeros términos, los términos constante y lineal son distintos de cero,
Si f(x) = 0
Si f (x) no es lineal, Xn + 1 es una aproximación mejorada de la raíz basada en la aproximación anterior Xn, la raíz será aproximada por esta iteración,
Mira También Carta Formal. Tipos, Estructura, Como Escribirla, Modelo
Carta Formal. Tipos, Estructura, Como Escribirla, ModeloRepresentación geométrica
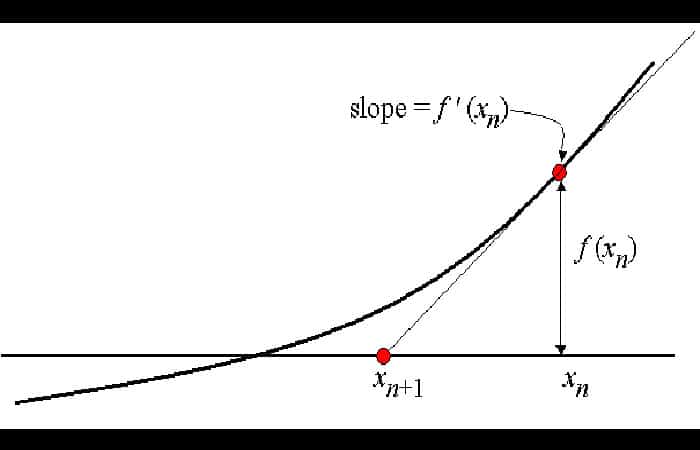
Aquí hay una imagen para demostrar lo que realmente hace el método de Newton:
Dibujamos una recta tangente a la gráfica de f (x) en el punto x = xnorte. Esta línea tiene pendiente F′ (xnorte) y pasa por el punto (x norte, f (x norte)). Por lo tanto tiene la ecuación y = F′ (xnorte)(x−xnorte)+f (xnorte).
Ahora, encontramos la raíz de esta línea tangente estableciendo y = 0 y xn + 1 para nuestra nueva aproximación. Resolver esta ecuación nos da nuestra nueva aproximación, que es:
 10 Tipos De Poemas Y Recursos Poéticos
10 Tipos De Poemas Y Recursos PoéticosEjemplo
Encuentra la raíz de la ecuación x ^ 2 - 4x - 7 = 0x2−4 x−7=0 cerca x = 5x =5 a la milésima más cercana.
Tenemos el nuestro x_0 = 5x0=5. Para utilizar el método de Newton, también necesitamos conocer la derivada de F. En este caso, f (x) = x ^ 2 - 4x - 7 y F′(x)=2 x−4. Usando el método de Newton, obtenemos la siguiente secuencia de aproximaciones:
Podemos detenernos ahora, porque los dígitos milésimo y diezmilésimo de x2 y x3 son lo mismo. Si continuáramos, seguirían siendo los mismos porque nos hemos acercado lo suficiente a la raíz:
Por tanto, nuestra respuesta final es 5.317.
Mira También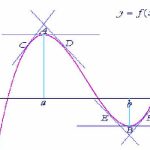 Cómo Encontrar El Mínimo Y El Máximo De Una Función
Cómo Encontrar El Mínimo Y El Máximo De Una FunciónTe invitamos a leer: ¿Cómo Saber Si Dos Vectores Son Paralelos?
Limitaciones del método de Newton
El método de Newton puede no funcionar si hay puntos de inflexión, máximos o mínimos locales alrededor x0 o la raíz. Por ejemplo, supon que necesitas encontrar la raíz de 27x ^ 3 - 3x + 1 = 02 o que está cerca x = 0. La respuesta correcta es -0,44157265….Sin embargo, el método de Newton le dará lo siguiente:
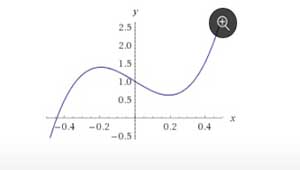
Claramente, esto no es útil. Eso es porque la gráfica de la función alrededor x = 0 se ve como esto:
Como puedes ver, este gráfico tiene un máximo local, un mínimo local y un punto de inflexión alrededor x=0. Para ver por qué el método de Newton no es útil aquí, imagina elegir un punto al azar entre x = -0.19 y x=−0.19 y trazar una línea tangente a la función en ese punto.
Mira También Gráfico Circular O Gráfico De Pastel. Qué Es, Usos Y Alternativas
Gráfico Circular O Gráfico De Pastel. Qué Es, Usos Y AlternativasEsa recta tangente tendrá una pendiente negativa y, por lo tanto, intersecará al eje en un punto más alejado de la raíz. En una situación como esta, ayudará a obtener un punto de partida aún más cercano, donde estos puntos críticos no interferirán.
Ejemplo
Resolvamos (2x ^ 3) -2x-1 = 0. En este caso f (x) = (2x ^ 3) -2x-1, entonces f ′ (x) = (6x ^ 2) -2. Entonces la fórmula se convierte en,
Necesitas decidir una suposición inicial apropiada x0 para este problema. F (1) = −1 <0 y f (2) = 11> 0. Por lo tanto, debe existir una raíz de f (x) = 0 entre 1 y 2. Tomemos x0 = 1 como nuestra suposición inicial. Luego
Y con x0 = 1 obtenemos x1 = 1,25.
Mira También Teorema Del Límite Central: Definición Y Ejemplos
Teorema Del Límite Central: Definición Y EjemplosAhora
Y con x1 = 1.25 obtenemos x2 = 1.1949. Para la siguiente etapa,
X3 = 1,1915. Continuando, encontramos que x4 = 1,191487884, x5 = 1,191487883, entre otros. Podemos detenernos cuando los dígitos dejen de cambiar al grado de precisión requerido. Concluimos que la raíz es 1,191487883.
Resumen de las particularidades del método de Newton Raphson
Cuando utilices el método de Newton Raphson debes tener en cuenta lo siguiente:
- Una estructura no lineal se puede analizar mediante una serie iterativa de aproximaciones lineales con correcciones.
- Algunos software utilizan un proceso iterativo llamado Método Newton-Raphson. Cada iteración se conoce como iteración de equilibrio.
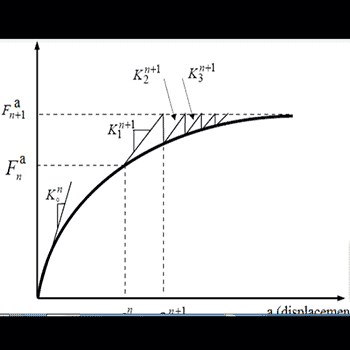
- En el análisis no lineal, la relación entre la carga y el desplazamiento no se puede determinar con una única solución basada en la rigidez inicial.
- Si las fuerzas residuales están dentro de una tolerancia aceptable, la solución converge.
- Si las fuerzas residuales no están dentro de una tolerancia aceptable, la solución no converge, por lo que se ensambla una nueva matriz de rigidez objetivo y se repite el proceso.
- En una solución no lineal, las iteraciones de equilibrio son soluciones correctivas necesarias para la convergencia mediante el método de Newton-Raphson.
Pensamientos finales
El método de Newton-Raphson es uno de los métodos más utilizados para encontrar raíces. Se puede generalizar fácilmente al problema de encontrar soluciones de un sistema de ecuaciones no lineales, que se conoce como técnica de Newton. Además, se puede demostrar que la técnica es cuadráticamente convergente a medida que nos acercamos a la raíz.
Echa un vistazo a: Ley De Distribución Normal – Qué Es Y Cómo Utilizarla
A diferencia de los métodos de bisección y posición falsa, la técnica de Newton-Raphson (NR) requiere solo un valor inicial x 0, al que nos referiremos como la estimación inicial de la raíz. Para ver cómo funciona el método NR, podemos reescribir la función f (x) usando una expansión de la serie de Taylor en (x - x0). Es una forma de encontrar rápidamente una buena aproximación para la raíz de una función de valor real f(x) = 0.
Antes de usar cualquiera de los métodos, deberíamos intentar obtener el mejor análisis posible para la función. Se puede desarrollar una idea aproximada de las raíces a partir de la física que representa la ecuación, el análisis matemático preliminar y el uso de rutinas de trazado.
Deja una respuesta


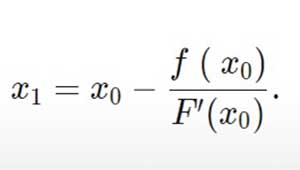
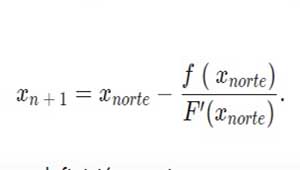
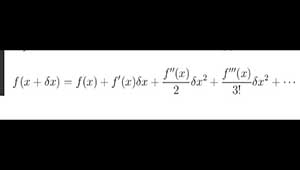
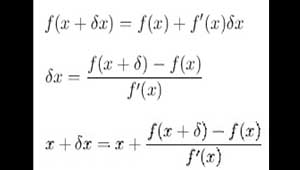

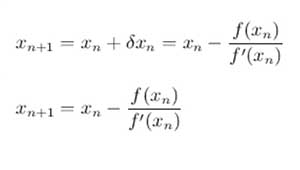




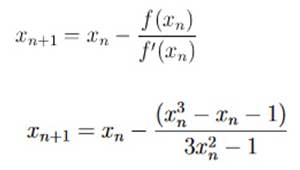
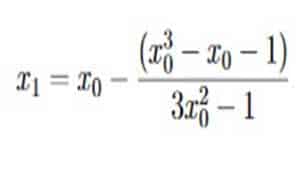
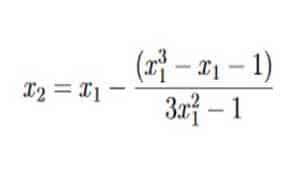
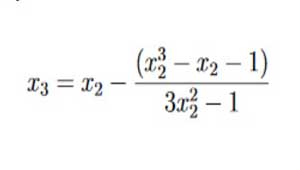
►TAMBIÉN DEBERÍAS LEER...