Ley De Distribución Normal – Qué Es Y Cómo Utilizarla
¿Te gustaría saber qué es la ley de distribución normal y cómo usarla? En esta ocasión te enseñaremos con ejemplos la ley de distribución normal también conocida como Ley gaussiana. Te invitamos a quedarte con nosotros.
La ley de distribución normal
Esta ley es muy usada para determinar el proceso implícito de las variantes aleatorias de los datos. Aquí te mostramos cómo usarla con ejemplos. Veamos:
Aquí puedes leer sobre: Cómo Funciona un Georadar.
Ley de distribución normal o gaussiana
Vamos a suponer que extraemos muestras aleatorias de una población cuyo tamaño promedio es de 170 cm, con una desviación estándar de 10 cm. Entoces, hay que dibujar el histograma del tamaño, con clases de 5 cm de ancho, para muestras cada vez más grandes.
Veamos cómo se ven estos histogramas:
 Importancia Del Gerente De Compras En Las Empresas
Importancia Del Gerente De Compras En Las EmpresasTamaño de la muestra:
- 10
- 100
- 000
- 000
- 000
Para este ejemplo, las clases son de 2 cm.
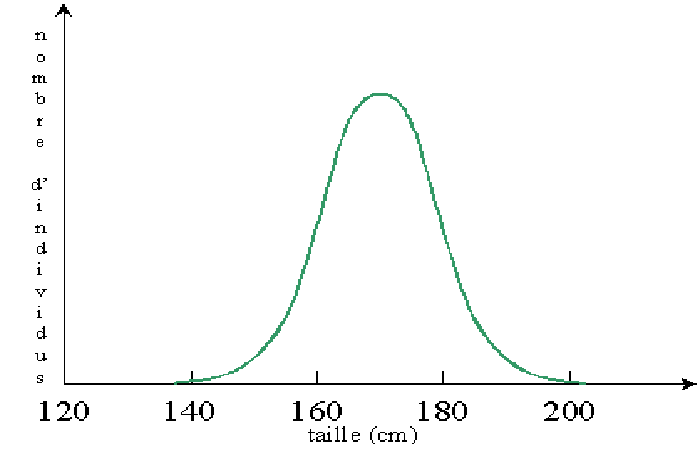
A medida que aumenta el tamaño de la muestra (y el tamaño de la clase disminuye), el histograma se vuelve cada vez más regular y se aproxima a una curva de campana, llamada ley de distribución normal.
Esta curva también se llama ley de Gauss, en honor al gran matemático alemán Karl Friederich Gauss (1777-1855).
La ley de distribución normal es la ley estadística más extendida y útil.
Representa muchos fenómenos aleatorios. Además, la ley de distribución normal puede aproximar muchas otras leyes estadísticas, especialmente en el caso de muestras grandes. Su expresión matemática es la siguiente:
Mira También 7 Técnicas Para Encontrar Temas Para Investigar
7 Técnicas Para Encontrar Temas Para Investigar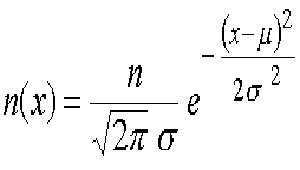
Esto se representa de la siguiente forma:
- es el promedio
- la desviación estándar
- n el número total de individuos en la muestra
- n (x) el número de individuos para los que la cantidad analizada tiene el valor x.
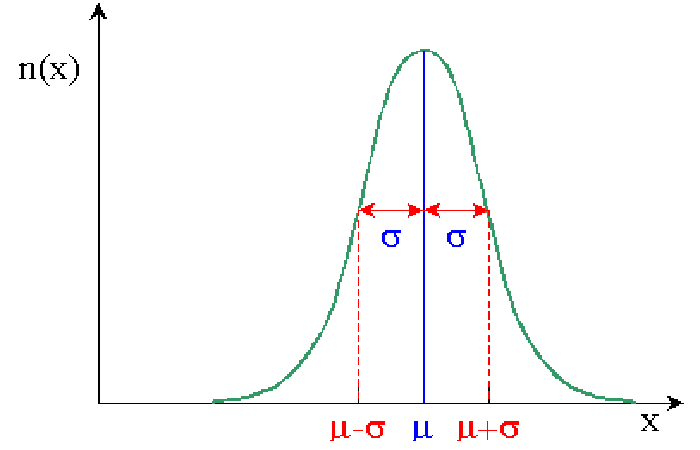
Cuando la distribución de individuos en una población obedece a la ley de distribución normal, encontramos:
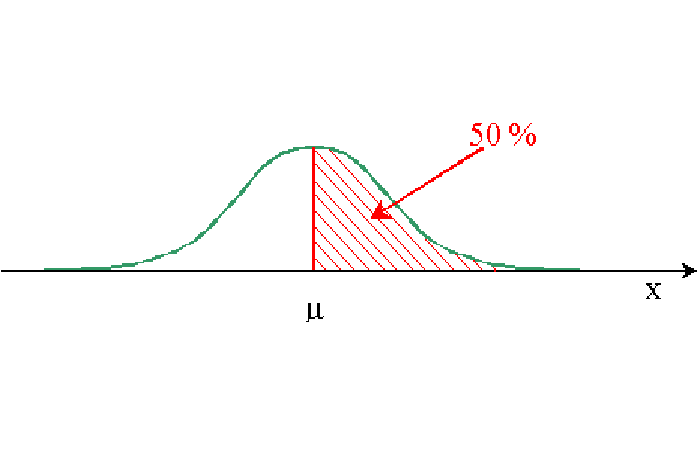
- 50% de individuos por debajo de la media y 50% por encima (la distribución normal es simétrica)
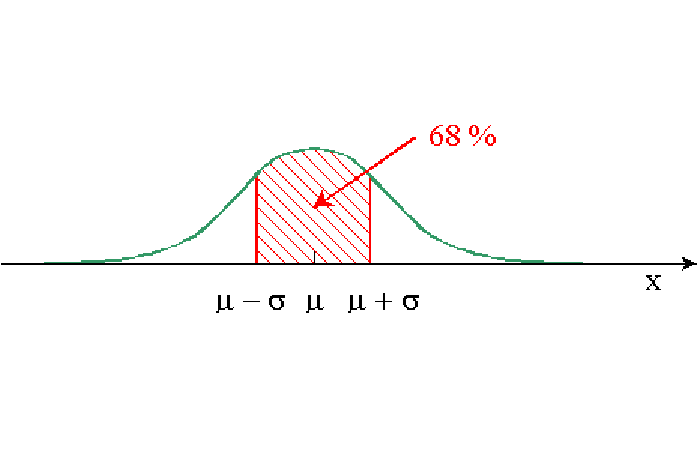
- 68% de las personas entre - y +
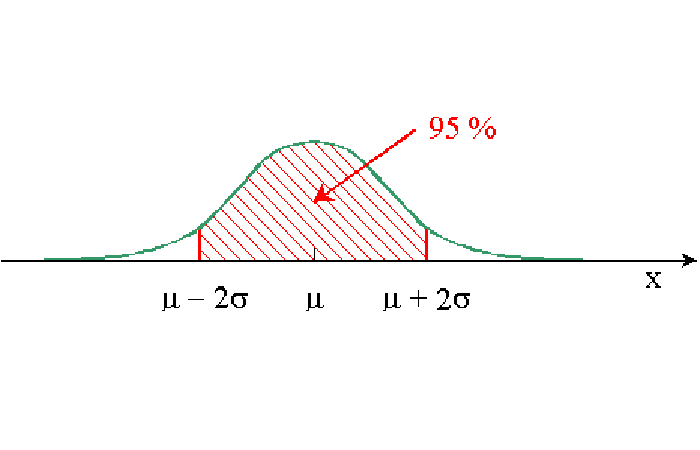
- 95% de los individuos entre -1,96 y 1,96 , que vamos a ronda al intervalo [ -2 , 2 ]
- 99,7% de las personas entre -3 y +3 (por lo tanto, hay muy pocas posibilidades de que una persona se desvíe de la media en más de 3 ).
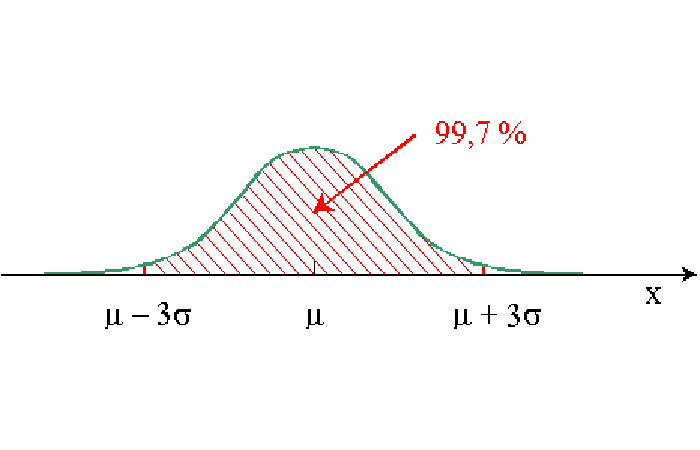
Cálculo de probabilidades
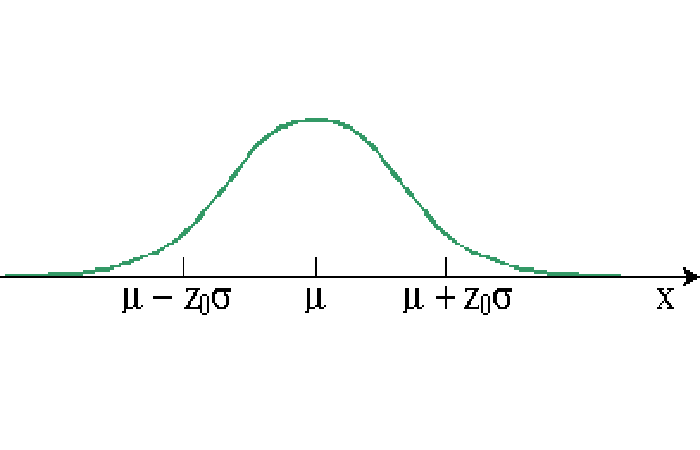
Para calcular las probabilidades asociadas con la distribución normal, generalmente usamos la distribución normal reducida: es una distribución normal para la cual = 0 y = 1. La siguiente tabla se utiliza para determinar la probabilidad de que la variable x se desvíe de la media en más de z 0 × hacia arriba. Para obtener z 0 , calculamos la desviación de la media:
= x - , luego lo dividimos por la desviación estándar:
|
2 º decimal z 0 |
||||||||||||
| Z 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 0,0 0,1 0,2 0,3 0,4 |
.500 .460 .421 .382 .345 |
.496 .456 .417 .378 .341 |
.492 .452 .413 .374 .337 |
.488 .448 .409 .371 .334 |
.484 .444 .405 .367 .330 |
.480 .440 .401 .363 .326 |
.476 .436 .397 .359 .323 |
.472 .433 .394 .356 .319 |
.468 .429 .390 .352 .316 |
.464 .425 .386 .348 .312 |
||
| 0,5 0,6 0,7 0,8 0,9 |
.309 .274 .242 .212 .184 |
.305 .271 .239 .209 .181 |
.302 .268 .236 .206 .179 |
.298 .264 .233 .203 .176 |
.295 .261 .230 .200 .174 |
.291 .258 .227 .198 .171 |
.288 .255 .224 .195 .169 |
.284 .251 .221 .192 .166 |
.281 .248 .218 .189 .164 |
.278 .245 .215 .187 .161 |
||
| 1,0 1,1 1,2 1,3 1,4 |
0,159 0,136 0,115 0,097 0,081 |
.156 .133 .113 .095 .079 |
.154 .131 .111 .093 .078 |
0,152 0,129 0,109 0,092 0,076 |
.149 .127 .107 .090 .075 |
.147 .125 .106 .089 .074 |
.145 .123 .104 .087 .072 |
.142 .121 .102 .085 .071 |
.140 .119 .100 .084 .069 |
.138 .117 .099 .082 .068 |
||
| 1,5 1,6 1,7 1,8 1,9 |
.067 .055 .045 .036 .029 |
.066 .054 .044 .035 .028 |
.064 .053 .043 .034 .027 |
.063 .052 .042 .034 .027 |
.062 .051 .041 .033 .026 |
.061 .049 .040 .032 .026 |
.059 .048 .039 .031 .025 |
.058 .047 .038 .031 .024 |
.057 .046 .038 .030 .024 |
.056 .046 .037 .029 .023 |
||
| 2,0 2,1 2,2 2,3 2,4 |
.023 .018 .014 .011 .008 |
.022 .017 .014 .010 .008 |
.022 .017 .013 .010 .008 |
.021 .017 .013 .010 .008 |
.021 .016 .013 .010 .007 |
.020 .016 .012 .009 .007 |
.020 .015 .012 .009 .007 |
.019 .015 .012 .009 .007 |
.019 .015 .011 .009 .007 |
.018 .014 .011 .008 .006 |
||
| 2,5 2,6 2,7 2,8 2,9 |
.006 .005 .003 .003 .002 |
.006 .005 .003 .002 .002 |
.006 .004 .003 .002 .002 |
.006 .004 .003 .002 .002 |
.006 .004 .003 .002 .002 |
.005 .004 .003 .002 .002 |
.005 .004 .003 .002 .002 |
.005 .004 .003 .002 .001 |
.005 .004 .003 .002 .001 |
.005 .004 .003 .002 .001 |
||
Esta probabilidad también se puede calcular mediante fórmulas aproximadas, que son más fáciles de manejar. Uno de ellos se implementa a continuación. Su precisión es muy buena (el error es como máximo 0,000015).
NOTA: No se consideran las probabilidades inferiores a 10 -10 = 10-10 (una diez mil millonésima). Se reemplazan por cero.
Cuando tenemos que determinar una probabilidad a partir de la distribución normal, intentamos reducirnos a una probabilidad considerada en la tabla.
A continuación se ilustran algunos casos concretos,
Ejemplos de uso de la ley de distribución normal:
El peso de los tomates producidos por un jardinero obedece a una ley de distribución normal de 200 gr de media y desviación estándar de 40 gr.
Mira También Tutorial para hacer un sombrero loco de niña en casa.
Tutorial para hacer un sombrero loco de niña en casa.- Calcula la probabilidad de que el peso de un tomate supere los 250 gr.
Solución:
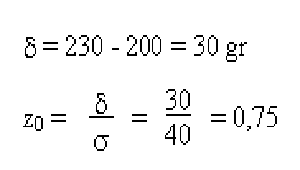
- Calcula la probabilidad de que el peso de un tomate sea inferior a 100 gr
Solución:
la distribución normal es simétrica no cuidamos el signo
Menos de 100 gr: por lo tanto, nos desviamos del valor medio = 200 gr en más de z 0
Prob = 0,006 = 0,6%
- Calcula la probabilidad de que el peso de un tomate sea inferior a 230 gr.
Solución:
Mira También 10 Mejores Páginas Webs Para Resolver Problemas Matemáticos
10 Mejores Páginas Webs Para Resolver Problemas Matemáticos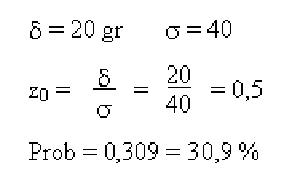
El intervalo (<230 gr) considerado contiene el valor medio (200 gr) que tomamos 1 - Prob (tabla):
- Prob = 1 - 0,227 = 0,773 = 77,3%
Calcula la probabilidad de que el peso de un tomate no se desvíe del valor medio en más de 20 gr.
Solución: primero calculamos la probabilidad de que el peso se desvíe en más de 20 gr, hacia arriba o hacia abajo:
Debemos multiplicar por 2 porque consideramos los dos lados. Prob = 2 × 0.309 = 0.618
Por lo tanto, tenemos un problema de 0.618 que el peso se desvía de más de 20 gr, y por lo tanto un problema. 1 - 0.618 que el peso no se desvíe más de 20 gr.
Respuesta: 0.382 = 38.2%
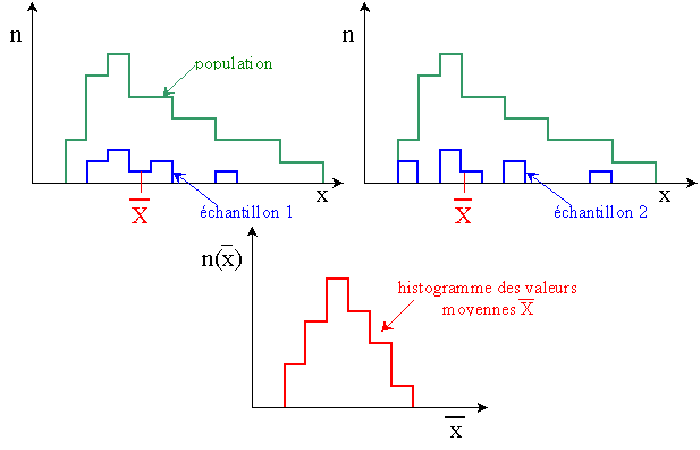
Forma de la distribución muestral
Suponga que analizamos cualquier población de un conjunto de muestras.
Para cada una de estas muestras, calculamos un valor promedio que es una estimación de la media de la población.
Por supuesto, las estimaciones generalmente diferirán del promedio real Queremos saber cómo se distribuirán las diferentes determinaciones alrededor de la media real.
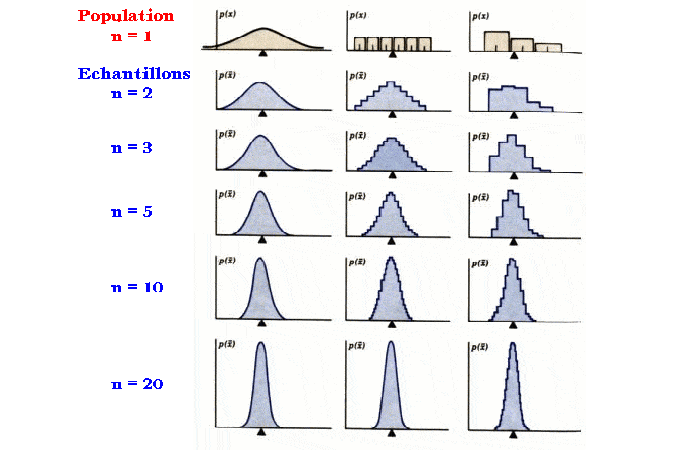
La siguiente figura muestra el histograma de los valores medios para muestras de tamaños crecientes extraídas de las poblaciones indicadas en la primera fila.
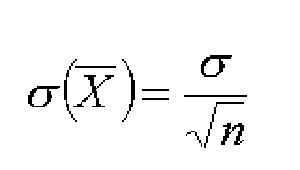
NOTA: Cuando el tamaño de la muestra es lo suficientemente grande (n 10), la distribución de la media tiene una forma aproximadamente normal.
La desviación estándar de la media es:
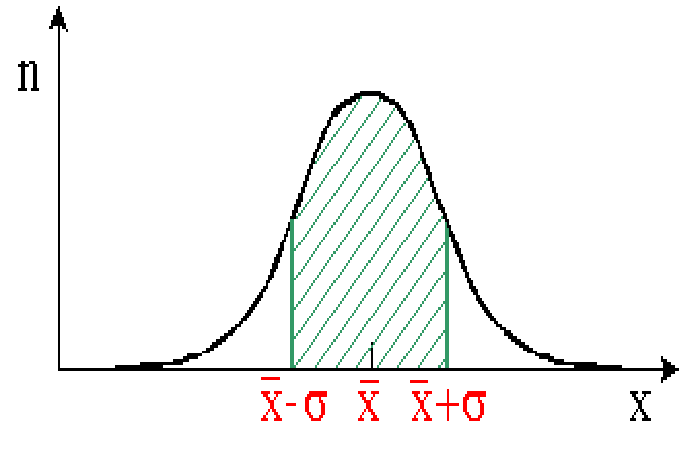
Independientemente de la población subyacente, si se utilizan muestras suficientemente grandes (al menos 10-20 individuos), la precisión del valor medio se puede calcular a partir de la distribución normal.
Existe un 68% ( 2/3) de probabilidad de que la media real esté en el rango entre y .
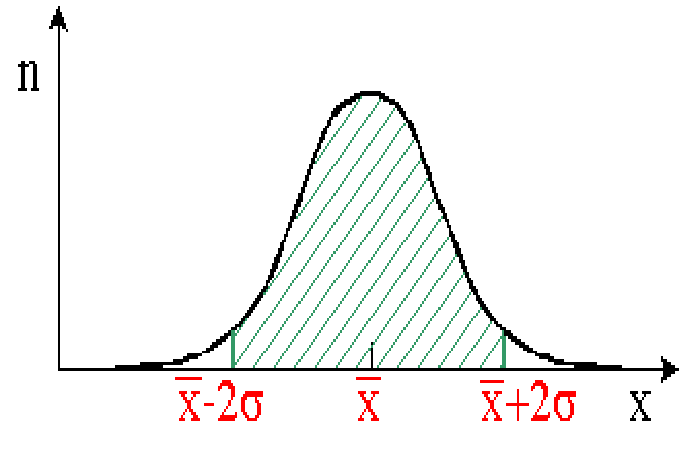
Existe una probabilidad del 95% de que la media real esté en el rango entre y .
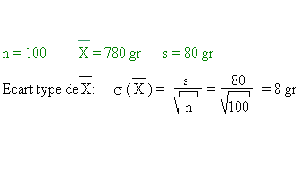
Ejemplos de:
- Una organización de consumidores desea saber si el peso real de las hogazas de 800 g producidas en una panadería está de acuerdo con el peso anunciado. Para ello, toma 100 panes al azar. Obtiene un peso medio de 780 gr, con una desviación estándar de 80 gr.
- ¿Cuál es la probabilidad de que el panadero engañe en promedio con el peso de su pan?
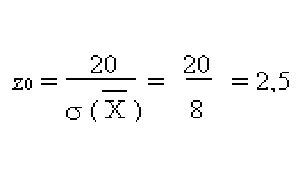
No hay trampa si es de 800 gr o menos, es decir 20 gr por encima.
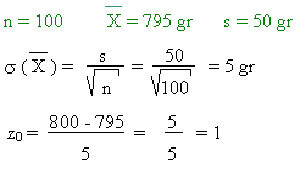
De la tabla, la probabilidad de que sea mayor que al menos 2.5 es 0.006.
100 - 100 × 0,006 = 100 - 0,6 = 99,4%
Hay un 99,4% de probabilidad de que el panadero esté haciendo trampa,
¡podemos concluir razonablemente que está haciendo trampa!
- En otra panadería, la muestra de 100 panes conduce al siguiente resultado:
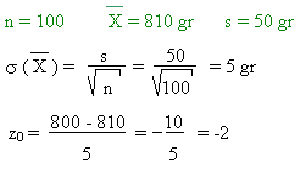
Según la tabla, la probabilidad de que sea mayor o igual a 800 gr es de 0,159, por lo que existe un 84,1% de probabilidad de que este panadero haga trampa. Incluso si la presunción es fuerte, ¡no es suficiente para concluir que está haciendo trampa!
- En una tercera panadería obtenemos:
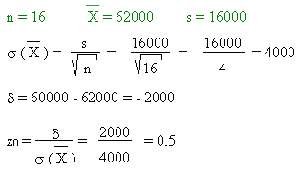
Según la tabla, la probabilidad de que sea menor o igual a 800 gr es de 0,023. Solo hay un 2,3% de posibilidades de que el panadero haga trampa.
¡Podemos concluir que es honesto!
- El ingreso promedio de una muestra representativa de 16 hogares asciende a 62,000 F netos por mes, con una desviación estándar de 16,000 F.
¿Cuál es la probabilidad de que el ingreso promedio de toda la población sea inferior a 60 000 F?
Solución:
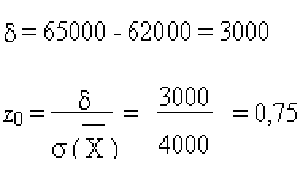
<60,000: se desvía en más de 0.5 × tomamos el valor de la tabla
- Prob = 0,309 = 30,6%
¿Cuál es la probabilidad de que el ingreso promedio de la población sea inferior a 65 000 F?
Solución:
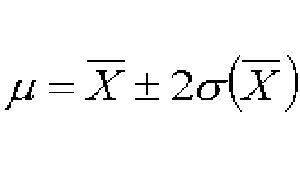
<65.000: No nos desviamos más de 0,75 × hacia arriba
Tomamos el valor P de la tabla y calculamos 1-P
P = 0,227
1-P = 0,773 = 77,3%
Intervalos de confianza
Hemos visto que la media de una muestra aleatoria permite estimar la media real de la población. También nos gustaría estimar la precisión de esta media, es decir, dar un margen de error o un intervalo de confianza. Podemos utilizar las tablas de distribución normal para estimar estos intervalos de confianza.
En general adoptaremos el intervalo de confianza è 95%, es decir è 2 ( ). Por lo tanto, podemos escribir, ya sea
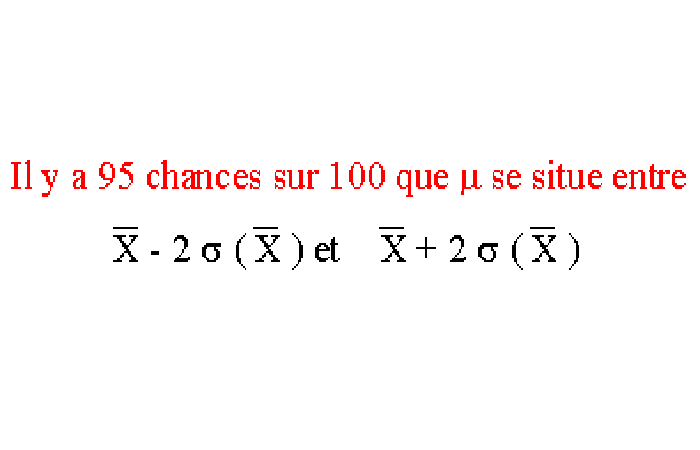
O, más explícitamente:
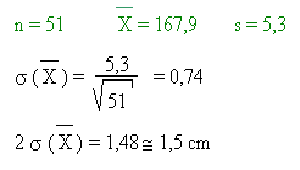
Si tomamos una serie de muestras de la población, en 19 de los 20 casos (en promedio), estará dentro del intervalo de confianza ± 2 ( ).
Ejemplos:
- El tamaño medio de una muestra de 51 niñas de 2º candi. commu. mide 167,9 cm. La desviación estándar de esta muestra es de 5,3 cm. Si asumimos que esta muestra es representativa del tamaño de las chicas belgas veinteañeras, podemos calcular el tamaño medio de esta población, con su margen de error:
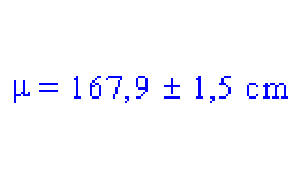
Por tanto, con un 95% de confianza, podemos decir que el tamaño medio de la población es:
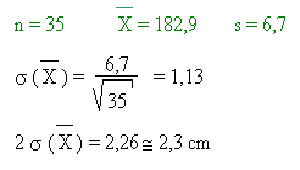
Lo que equivale a decir que hay 95 posibilidades sobre 100 de que la estatura media de las chicas belgas de 20 años esté entre 166,4 y 169,4 cm. El tamaño promedio de una muestra de 35 niños de 2º candi. commu. Mide 182,9 cm.
Suponiendo de manera similar la muestra representativa, podemos dar un intervalo de confianza para la altura de los niños belgas de 20 años
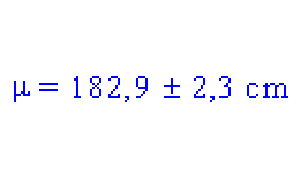
Por lo tanto, con un 95% de confianza, tenemos:
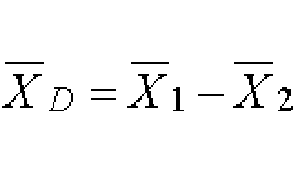
Comparación de dos muestras independientes
Las muestras son independientes cuando una modificación en una de ellas no influye en las demás.
Por ejemplo, una muestra de niñas y una muestra de niños seleccionados para determinar el peso medio de las niñas y el de los niños son independientes.
Por otro lado, las personas que dicen votar por un partido A o un partido B en una encuesta política no forman dos muestras independientes porque si una persona más declara votar por A, hay un votante potencial menos por B (los resultados de A y B se influyen mutuamente).
Si tenemos 2 muestras independientes, de medias 1 y 2 , con desviaciones estándar de estas medias, 1 ( ) y 2 ( ), podemos estimar la diferencia de las medias, así como la desviación estándar de esta diferencia.
La diferencia promedio es simplemente:
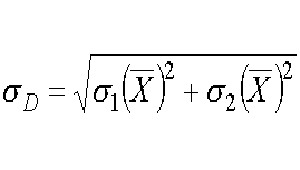
Su desviación estándar viene dada por:
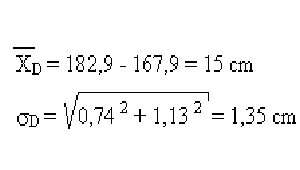
(fórmula aproximada, pero suficientemente precisa)
Para el tamaño de niñas y niños, obtenemos:
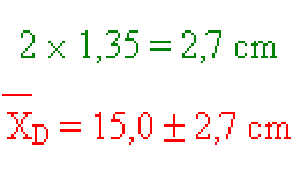
El intervalo de confianza del 95% es:
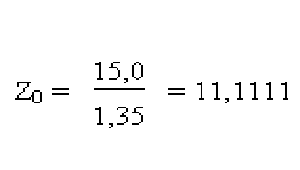
Si ahora queremos responder a la siguiente pregunta: ¿son los niños más altos, en promedio, que las niñas?
- diferencia de tamaño promedio: D = 15.0 cm
- desviación estándar de esta diferencia: D = 1,35 cm
- número de desviaciones estándar por encima de 0 cm (0 cm sin diferencia de tamaño)
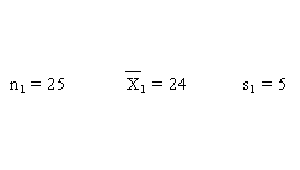
En una distribución normal, la probabilidad de tener un valor que se desvíe de la media en más de 11 es menor que 2,10 -28 y, por lo tanto, completamente despreciable.
Si nuestras muestras son representativas, entonces no hay posibilidad de que la diferencia de tamaño se deba al azar.
Según nuestras muestras, por lo tanto, estamos prácticamente seguros de que los niños son, en promedio, más altos que las niñas.
Ejemplo
Se selecciona una muestra de 25 campesinos sildavianos. Su área de tierra promedia 24 hectáreas, con una desviación estándar de 5 hectáreas.
Para una muestra de 16 agricultores fronterizos, el área de tierra promedio es de 26 hectáreas, con una desviación estándar de 8 hectáreas.
¿Cuál es la probabilidad de que los campesinos de Syldavia tengan, en promedio, más tierra que las fronteras?
Solución:
- Muestra de Syldavian:
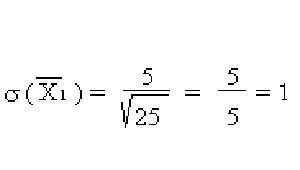
- Desviación estándar de la media:
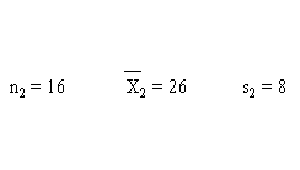
- Muestra de borde:
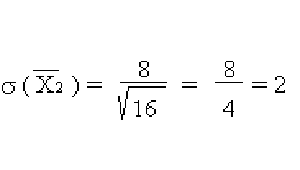
- Desviación estándar de la media:
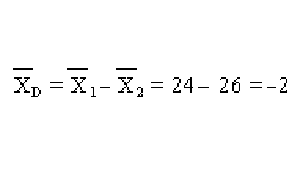
- Diferencia media: (frontera de Sildavia):
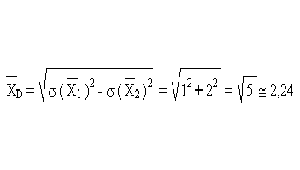
- Desviación estándar de la diferencia:
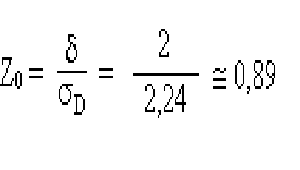
- los habitantes de Sildavia tienen más tierra en promedio que las fronteras si la diferencia es> 0 se desvía del valor medio calculado en más de 2
Tabla Prob = 0,187 = 18, 7% posibilidad de que el área promedio sea más alta en Syldavia.
¿Cómo redondear?
No existe una receta absoluta para redondear correctamente.
Redondear demasiado puede provocar una pérdida de precisión.
El redondeo demasiado pequeño sugiere una precisión ilusoria y reduce la legibilidad de los resultados.
La receta sugerida a continuación es un buen compromiso entre los dos extremos.
Para no perder precisión, especialmente en cálculos largos, es recomendable redondear solo al final, al presentar los resultados
Sobre el margen de error (en general): mantenga 2 dígitos significativos.
Es decir, empezando por la izquierda, el primer dígito distinto de 0 y el siguiente.
El último dígito significativo que mantenemos se redondea hacia abajo o hacia arriba para que el valor redondeado sea el más cercano al valor calculado:
hacia abajo si el siguiente dígito es 0, 1, 2, 3 o 4;
hacia arriba si el siguiente dígito es 5, 6, 7, 8 o 9;
Ejemplos
| redondeo correcto | |
| 35,2438 2379 0,6694 0,0023256 0,0004041 0,89712 |
35 2400 0,67 0,0023 0,00040 0,90 |
Sobre el resultado afectado por un cierto margen de error : mantener el mismo número de decimales que para .
Ejemplos
| resultados | resultado redondeado | |
| 1864.387 0.68088 24.52698 2624.57 54867.12 |
6,8 0,013 0,25 120 2000 |
1.864,4 0.681 24,53 2.620 54.900 |
(En el último caso, el dígito de las centenas de es significativo porque, aunque es 0, sigue al primer dígito distinto de cero).
También puedes aprender sobre: Licenciado En Matemáticas. Que Es, Donde Estudiar, Costos, Duración
Conclusión
Como puedes ver, esta es la manera en la que puedes usar la ley de distribución normal para realizar tu cálculos promédiales. Te recomendamos leer detenidamente para que puedas aplicar la ley de gaussiano. Esperamos haberte ayudado con esta información
Deja una respuesta

►TAMBIÉN DEBERÍAS LEER...