Teorema Del Límite Central: Definición Y Ejemplos
¿Te gustaría saber qué es el teorema del límite central y cómo se aplica? Aquí te dejaremos la definición y algunos ejemplos que puedes usar cuando quieras establecer medidas y aproximaciones de muestras y tamaños. Te invitamos a quedarte con nosotros
¿Qué es el teorema del límite central?
El teorema del límite central establece que la distribución muestral de las medias muéstrales se aproxima a una distribución normal a medida que aumenta el tamaño de la muestra, sin importar la forma de la distribución de la población. Este hecho es especialmente cierto para tamaños de muestra superiores a 30.
Aquí puedes aprender sobre: Ley De Distribución Normal – Qué Es Y Cómo Utilizarla
Todo lo que esto dice es que a medida que tome más muestras, especialmente las grandes, su gráfico de las medias muéstrales se parecerá más a una distribución normal.
Esto es lo que dice gráficamente el teorema del límite central. La siguiente imagen muestra uno de los tipos de prueba más simples: lanzar un dado justo. Cuantas más veces se lanza el dado, es más probable que la forma de la distribución de las medias se parezca a un gráfico de distribución normal.
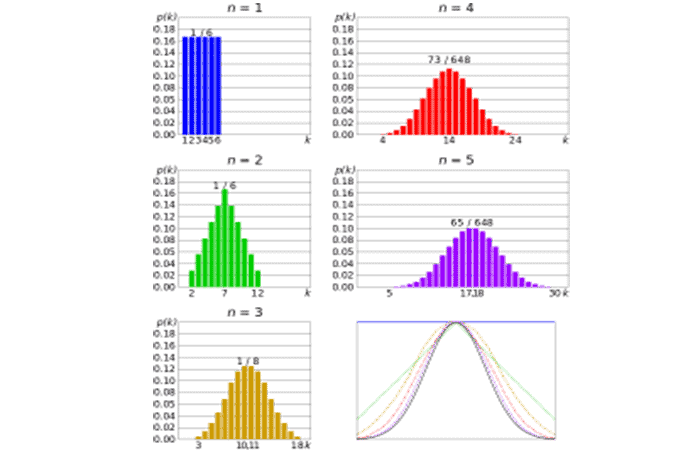
El teorema y las medias del límite central
Un componente esencial del Teorema del límite central es que el promedio de las medias muéstrales será la media de la población. En otras palabras, sume las medias de todas sus muestras, encuentre el promedio y ese promedio será la media real de su población.
Mira También Qué Es El Paquete De Software SAP Y Cómo Funciona
Qué Es El Paquete De Software SAP Y Cómo FuncionaDe manera similar, si encuentra el promedio de todas las desviaciones estándar en su muestra, encontrará la desviación estándar real para su población. Es un fenómeno bastante útil que puede ayudar a predecir con precisión las características de una población.
Definición mediante cálculo
Si ha realizado algún cálculo, puede definir el CLT con mayor precisión utilizando la definición de un límite. La CDF de la media muestral estandarizada (X̄ - μ) / σ converge puntualmente a la CDF (Φ) de la distribución normal estándar. Esto se muestra con la integral: Donde:
- X n es una secuencia IID
- Φ (z) = ℙ (Z ≤ z) =
NOTA: Una suposición es que el valor esperado de X y X 2 < infinito.
Ejemplos del teorema del límite central
Un problema verbal del Teorema del límite central probablemente contendrá la frase “suponga que la variable está distribuida normalmente”, o una similar. Con estos ejemplos del teorema del límite central, se te dará:
Mira También Diseño Y Medidas De Una Tarjeta De Presentación
Diseño Y Medidas De Una Tarjeta De Presentación- Una población (es decir, hombres de 29 años, personas mayores entre 72 y 76, todos los vehículos registrados, todos los dueños de gatos)
- Un promedio (es decir, 125 libras, 24 horas, 15 años, $ 15,74)
- Una desviación estándar (es decir, 14,4 libras, 3 horas, 120 meses, $ 196,42)
- Un tamaño de muestra (es decir, 15 hombres, 10 personas mayores, 79 automóviles, 100 hogares)
Ejemplos del teorema del límite central: mayor que
Para problemas verbales del Teorema del límite central que contienen la frase “mayor que” (o una frase similar como “arriba”).
Pasos generales
- Paso 1: Identifica las partes del problema. Tu pregunta debe indicar:
- la media (promedio o μ)
- la desviación estándar (σ)
- tamaño de la población
- tamaño de muestra (n)
- un número asociado con "mayor que".
NOTA: esta es la media de la muestra. En otras palabras, el problema le pregunta: “¿Cuál es la probabilidad de que una media muestral de x elementos sea mayor que este número?
- Paso 2:Dibuja una gráfica. Rotula el centro con la media. Sombrea el área aproximadamente por encima (es decir, el área "mayor que"). Este paso es opcional, pero puede ayudarte a ver lo que estás buscando.
- Paso 3:usa la siguiente fórmula para encontrar el puntaje z. Ingresa los números del paso 1.
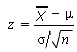
- Resta la media (μ en el paso 1) del valor 'mayor que' (en el paso 1). Deja este número a un lado por un momento.
- Divide la desviación estándar (σ en el paso 1) por la raíz cuadrada de su muestra (n en el paso 1). Por ejemplo, si treinta y seis niños están en tu muestra y su desviación estándar es 3, entonces 3 / √36 = 0.5
- Divide tu resultado del paso 1 por tu resultado del paso 2 (es decir, paso 1 / paso 2)
- Paso 4: busca la puntuación z que calculó en el paso 3 en la tabla z.
- Paso 5: Resta tu puntaje z de 0.5. Por ejemplo, si tu puntaje es 0.1554, entonces 0.5 - 0.1554 = 0.3446.
- Paso 6:Convierta el decimal en el Paso 5 a un porcentaje. En este ejemplo, 0.3446 = 34.46%.
Ejemplo específico
Un cierto grupo de beneficiarios de asistencia social recibe beneficios SNAP de $ 110 por semana con una desviación estándar de $ 20. Si se toma una muestra aleatoria de 25 personas, ¿cuál es la probabilidad de que su beneficio medio sea superior a $ 120 por semana?
- Paso 1: Inserta la información en la fórmula z:
- = (120-110) / 20 √25 = 10 / (20/5) = 10/4 = 2.5.
- Paso 2: busca el puntaje z en una tabla. Una puntuación z de 2,5 tiene un área de aproximadamente 49,38%. Sumando 50% (para la mitad izquierda de la curva), obtenemos 99,38%.
Ejemplos del teorema del límite central: menor que
Resolver problemas verbales del Teorema del límite central que contienen la frase "menor que" (o una frase similar como "inferior").
Mira También Ejemplo De Orden De Compra Con Instrucciones De Uso
Ejemplo De Orden De Compra Con Instrucciones De UsoPasos generales
- Paso 1: Identifica las partes del problema. Tu pregunta debe indicar:
- la media (promedio o μ)
- la desviación estándar (σ)
- tamaño de la población
- tamaño de muestra (n)
- un número asociado con "menor que"
- Paso 2: Dibuja una gráfica. Rotula el centro con la media. Sombrea el área aproximadamente debajo (es decir, el área "menor que"). Este paso es opcional, pero puede ayudarte a ver lo que estás buscando.
- Paso 3: usa la siguiente fórmula para encontrar el puntaje z. Ingresa los números del paso 1.
Si las fórmulas te confunden, todo lo que esta fórmula te pide que hagas es:
- Reste la media (μ en el paso 1) del valor menor que (en el paso 1). Deje este número a un lado por un momento.
- Divida la desviación estándar (σ en el paso 1) por la raíz cuadrada de su muestra (n en el paso 1). Por ejemplo, si treinta y seis niños están en su muestra y su desviación estándar es 2, entonces 3 / √ 36 = 0.5
- Divida su resultado del paso 1 por su resultado del paso 2 (es decir, paso 1 / paso 2)
- Paso 4: busca la puntuación z que calculó en el paso 4 en la tabla z. Si no recuerda cómo buscar las puntuaciones z, puede encontrar una explicación en el paso 1 de este artículo sobre el área a la derecha de una puntuación z en una curva de distribución normal.
- Paso 5: agrega tu puntaje z a 0.5. Por ejemplo, si tu puntaje z es 0.1554, entonces 0.5 + 0.1554 es 0.6554.
- Paso 6: Convierta el decimal en el Paso 6 a un porcentaje. En nuestro ejemplo, 0,6554 = 65,54%.
Ejemplo específico
Una población de hombres de 29 años tiene un salario medio de $ 29,321 con una desviación estándar de $ 2,120. Si se toma una muestra de 100 hombres, ¿cuál es la probabilidad de que sus salarios medios sean inferiores a $ 29 000?
- Paso 1: Inserta los valores en la fórmula z:
- = (29,000 - 29,321) / (2,120 / √100) = -321/212 = -1.51.
- Paso 2: busca la puntuación z en la tabla z de la izquierda. -1,51 tiene un área de 93,45%.
Sin embargo, esta no es la respuesta, ya que la pregunta pide MENOS DE, y 93.45% es el área "mayor que", por lo que debe restar del 100%.
100% - 93,45% = 6,55% o aproximadamente 0,07.
Mira También Cómo Sacar El Promedio En Excel. 4 Métodos
Cómo Sacar El Promedio En Excel. 4 MétodosEjemplos del teorema del límite central: entre
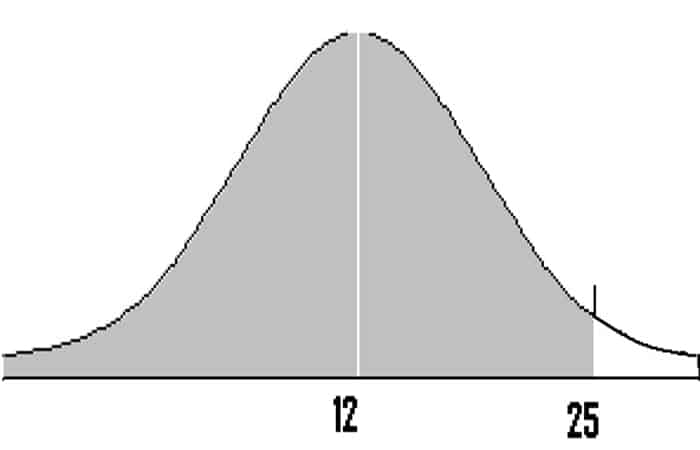
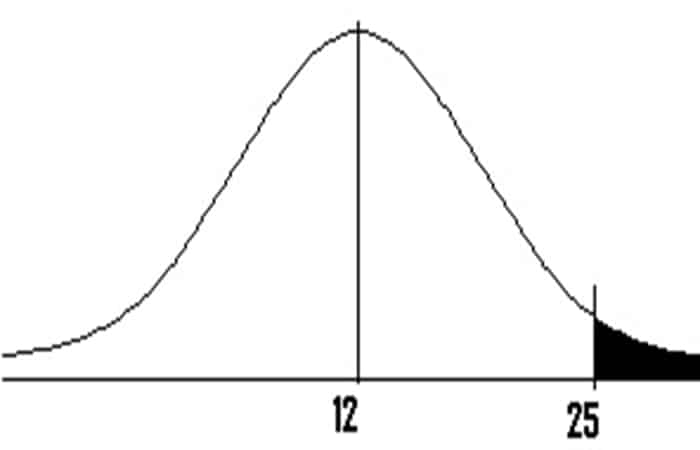
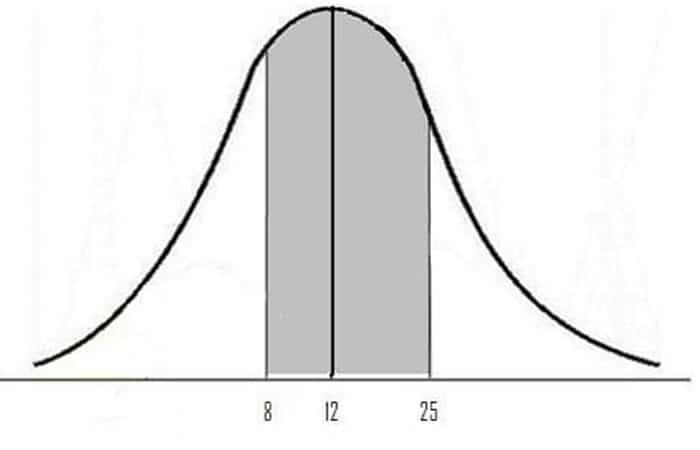
Problema de ejemplo: Hay 250 perros en una exposición canina que pesan un promedio de 12 libras, con una desviación estándar de 8 libras. Si se eligen 4 perros al azar, ¿cuál es la probabilidad de que tengan un peso promedio de más de 8 libras y menos de 25 libras?
- Paso 1: Identifica las partes del problema. Tu pregunta debe indicar:
- media (promedio o μ) desviación estándar (σ) tamaño de la población
- tamaño de muestra (n)
- número asociado con "menos de" 1
- número asociado con "mayor que" 2
- Paso 2: Dibuja una gráfica. Rotula el centro con la media. Sombrea el área entre 1 y 2. Este paso es opcional, pero puede ayudarte a ver lo que está buscando.
- Paso 3: usa la siguiente fórmula para encontrar las puntuaciones z. Todo lo que esta fórmula te pide que hagas es:
- Resta la media (μ en el paso 1) del valor mayor que (Xbar en el paso 1): 25 - 12 = 13.
- Divida la desviación estándar (σ en el paso 1) por la raíz cuadrada de su muestra (n en el Paso 1): 8 / √ 4 = 4
- Divide tu resultado de a por su resultado de b : 13/4 = 3.25
- Paso 4 Usa la fórmula del Paso 3 para encontrar los valores z. Esta vez, usa Xbar2 del paso 1 (8).
- Resta la media (μ en el Paso 1) del valor mayor que (X barra en el Paso 1): 8 - 12 = -4.
- Divide la desviación estándar (σ en el Paso 1) por la raíz cuadrada de tu muestra (n en el Paso 1): 8 / √ 4 = 4
- Divide tu resultado de a por tu resultado de b: -4 / 4 = -1
- Paso 5: Busca el valor que calculó en el Paso 3 en la tabla z.
- El valor Z de 3.25 corresponde a .4994
- Paso 6: Busca el valor que calculó en el Paso 4 en la tabla z.
- El valor Z de 1 corresponde a .3413
Ten en cuenta que la curva de campana es simétrica, por lo que si quieres buscar un valor negativo como -1, simplemente busca la contraparte positiva. El área será la misma.
- Paso 7: Suma los pasos 5 y 6 juntos:
- .4994 + .3413 = .8407
- Paso 8: Convierta el decimal en el Paso 7 a un porcentaje:
- 8407 = 84.07%
Teorema del límite central en la TI 89
Problema de ejemplo: una población de estudiantes de colegios comunitarios incluye estudiantes del centro de la ciudad (p = .33). ¿Cuál es la probabilidad de que una muestra aleatoria de 45 estudiantes de la población tenga entre un 20% y un 40% de estudiantes del centro de la ciudad?
- Paso 1: Presiona APLICACIONES. Resalta el editor de estadísticas / listas usando las teclas de desplazamiento. Presiona ENTER.
Si no ves el editor de estadísticas / listas, debes cargar la aplicación. - Paso 2: Presiona F5 y desplázate hacia abajo hasta C:BinomialCdf.
- Paso 3: Ingresa 45 en el cuadro Num Trials.
- Paso 4: Desplázate hacia abajo e Ingresa .33 en el cuadro Prob Success.
- Paso 5: Desplázate hacia abajo e Ingresa 9 en el cuadro Valor inferior (porque 20% de 45 = 9).
- Paso 6: Desplázate hacia abajo e Ingresa 18 en el cuadro Valor superior (porque 40% de 45 = 18). Presione ENTER.
- Paso 7: Lee el resultado: Cdf = .857142. Esto significa que la probabilidad de que su muestra aleatoria tenga entre un 20 y un 40% de estudiantes del centro de la ciudad es del 85,71%.
Teorema del límite central de la TI 83: descripción general
La calculadora TI 83 tiene una función incorporada que puede ayudarte a calcular las probabilidades de los problemas verbales del teorema central, que generalmente contienen la frase "suponga que la distribución es normal" (o una variación de esa frase).
La función, normalcdf, requiere que Ingresa un límite inferior, un límite superior, una media y una desviación estándar.
Problema de ejemplo: una empresa de fertilizantes fabrica fertilizante orgánico en bolsas de 10 libras con una desviación estándar de 1,25 libras por bolsa. ¿Cuál es la probabilidad de que una muestra aleatoria de 15 bolsas tenga una media de entre 9 y 9.5 libras?
Mira También Método De Newton Raphson. Cálculo Y Ejercicios Resueltos
Método De Newton Raphson. Cálculo Y Ejercicios Resueltos- Paso 1: 2do VARS 2.
- Paso 2: Ingresa tus variables (límite inferior, límite superior, media y desviación estándar). Separa cada variable con una coma: 9,9.5, 10, (1.25 / √15)).
- Paso 3: Presiona ENTER. Esto devuelve la probabilidad de .05969 o.05969%.
También te puede interesar leer sobre: 10 Mejores Páginas Webs Para Resolver Problemas Matemáticos
Sugerencia: Si tienes una pregunta que solicita “mayor que” o “menor que” un determinado número, Ingresa 999999999 para el límite inferior o superior. Por ejemplo, si quisiera saber la probabilidad de más de 8 libras, ingresaría:
- NORMALCDF (8, 999999999, 10, 1. / √ (15))
Menos de 8 libras, ingresaría:
- NORMALCDF (999999999,8,10 , 1. / √ (15))
Consejo: las distribuciones de muestreo requieren que la desviación estándar de la media sea σ / √ (n), así que asegúrese de ingresarla como desviación estándar.
Deja una respuesta

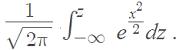
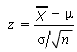
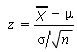
►TAMBIÉN DEBERÍAS LEER...