Análisis De Correlación. Qué Es, 2 Métodos Y Cómo Se Calcula
El análisis de correlación es un tema que pocas personas pueden recordar de las lecciones de estadística en la escuela, pero que la mayoría de los profesionales conocerá como un elemento básico del análisis de datos. Sin embargo, las correlaciones con frecuencia se malinterpretan y se usan de manera incorrecta, incluso en la industria de la información por varias razones. Así que aquí hay una guía útil sobre los conceptos básicos del análisis de correlación a lo largo del camino.
- ¿Qué es análisis de correlación?
- Usos del análisis de correlación
- Ventajas del análisis de correlación
- Coeficientes de correlación
- Cuándo usar cada método de cálculo
- Interpretación de resultados
- Usando un coeficiente de correlación
- Interpretar un coeficiente de correlación
- Visualización de correlaciones lineales
- Otros coeficientes
-
Preguntas frecuentes sobre los coeficientes de correlación
- ¿Qué es una correlación?
- ¿Cuántas variables hay en una correlación?
- ¿Qué es un coeficiente de correlación?
- ¿Cuáles son los supuestos del coeficiente de correlación de Pearson?
- ¿Qué te dicen el signo y el valor del coeficiente de correlación?
- ¿Es el coeficiente de correlación lo mismo que la pendiente de la recta?
- Pensamientos finales
¿Qué es análisis de correlación?
El análisis de correlación es un método estadístico que se utiliza para descubrir si existe una relación entre dos variables/conjuntos de datos y qué tan fuerte puede ser esa relación. En términos de investigación de mercado, esto significa que el análisis de correlación se utiliza para analizar datos cuantitativos recopilados a partir de métodos de investigación como encuestas y sondeos, para identificar si existen conexiones, patrones o tendencias significativas entre los dos.
Quizás te puede interesar: Mediadas De Tendencia Central. Cuáles Son, Cálculo Y Representación Gráfica
Se analizan datos cuantitativos para identificar si existen patrones, tendencias o conocimientos significativos. Esencialmente, el análisis de correlación se usa para detectar patrones dentro de conjuntos de datos. Un resultado de correlación positivo significa que ambas variables aumentan entre sí, mientras que una correlación negativa significa que a medida que una variable disminuye, la otra aumenta.
Usos del análisis de correlación
El análisis de correlación se utiliza para estudiar casos prácticos. Aquí, el investigador no puede manipular variables individuales. Por ejemplo, el análisis de correlación es usado para medir la correlación entre la presión arterial del paciente y la medicación utilizada. Los especialistas en marketing lo utilizan para medir la eficacia de la publicidad. Los investigadores miden el aumento/disminución de las ventas debido a una campaña de marketing específica.
Mira También Cómo Poner Un Video En PowerPoint. 2 Métodos
Cómo Poner Un Video En PowerPoint. 2 MétodosVentajas del análisis de correlación
Las ventajas del análisis de correlación son:
- Observar relaciones: una correlación ayuda a identificar la ausencia o presencia de una relación entre dos variables. Tiende a ser más relevante para la vida cotidiana.
- Un buen punto de partida para la investigación: demuestra ser un buen punto de partida cuando un investigador comienza a investigar las relaciones por primera vez.
- Usos para estudios posteriores: los investigadores pueden identificar la dirección y la fuerza de la relación entre dos variables y luego reducir los hallazgos en estudios posteriores.
- Métricas simples: los resultados de la investigación son fáciles de clasificar. Los resultados pueden oscilar entre -1,00 y 1,00. Solo puede haber tres posibles resultados amplios del análisis.
Coeficientes de correlación
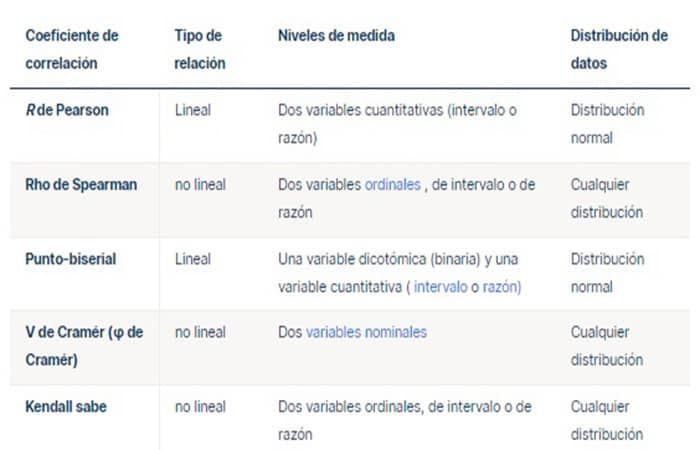
Por lo general, hay tres formas diferentes de clasificar la correlación estadística según Spearman, Kendall y Pearson. Cada coeficiente representará el resultado final como 'r'. El rango de Spearman y el coeficiente de Pearson son las dos fórmulas analíticas más utilizadas según los tipos de datos que los investigadores tienen a mano:
Coeficiente de correlación de rango de Spearman
Este coeficiente se usa para ver si existe alguna relación significativa entre los dos conjuntos de datos y opera bajo el supuesto de que los datos que se usan son ordinales, lo que aquí significa que los números no indican cantidad, sino que significan una posición de lugar de la posición del sujeto (p. ej., 1º, 2º, 3º, entre otros).
Este coeficiente requiere una tabla de datos que muestre los datos sin procesar, los rangos y la diferencia entre los dos rangos. Esta diferencia al cuadrado entre los dos rangos se mostrará en un gráfico de dispersión, que indicará claramente si existe una correlación positiva, una correlación negativa o ninguna correlación entre las dos variables.
Mira También Carta De Recomendación Para El Trabajo. Qué Es, 2 Ejemplos Y Plantillas
Carta De Recomendación Para El Trabajo. Qué Es, 2 Ejemplos Y PlantillasLa restricción bajo la que funciona este coeficiente es -1 ≤ r ≤ +1, donde un resultado de 0 significaría que no hay relación alguna entre los datos.
Fórmula del coeficiente de correlación de rango de Spearman
Los símbolos de la rho de Spearman son ρ para el coeficiente de población y r s para el coeficiente de muestra. La fórmula calcula el coeficiente de correlación r de Pearson entre las clasificaciones de los datos variables.
Para usar esta fórmula, primero clasificará los datos de cada variable por separado de menor a mayor: cada punto de datos recibe una clasificación del primero, segundo o tercero, y así sucesivamente.
Luego, encontrarás las diferencias (di) entre los rangos de las variables para cada par de datos y lo tomarás como la entrada principal para la fórmula. Explicación de la fórmula del coeficiente de correlación de rango de Spearman:
Mira También Gráfico Circular O Gráfico De Pastel. Qué Es, Usos Y Alternativas
Gráfico Circular O Gráfico De Pastel. Qué Es, Usos Y Alternativas- rs = fuerza de la correlación de rango entre variables.
- di = la diferencia entre el rango de la variable x y el rango de la variable y para cada par de datos
- ∑d2i = suma de las diferencias al cuadrado entre los rangos de las variables “x” y “y”
- n = tamaño de la muestra
Si tienes un coeficiente de correlación de 1, todas las clasificaciones de cada variable coinciden para cada par de datos. Si tienes un coeficiente de correlación de -1, las clasificaciones de una variable son exactamente opuestas a las clasificaciones de la otra variable. Un coeficiente de correlación cercano a cero significa que no existe una relación monótona entre las clasificaciones de las variables.
Coeficiente producto-momento de Pearson
Esta es la fórmula de análisis de correlación más utilizada, que mide la fuerza de las relaciones ' lineales ' entre los datos sin procesar de ambas variables, en lugar de sus rangos. Se trata de un coeficiente adimensional, lo que significa que no hay límites relacionados con los datos que deban considerarse al realizar análisis con esta fórmula, razón por la cual este coeficiente es el primero que prueban los investigadores.
Sin embargo, si la relación entre los datos no es lineal, entonces es cuando este coeficiente en particular no representará con precisión la relación entre las dos variables, y cuando se debe implementar el Rango de Spearman en su lugar.
El coeficiente de Pearson requiere que los datos relevantes se ingresen en una tabla similar a la del rango de Spearman pero sin los rangos, y el resultado producido tendrá la forma numérica que producen todos los coeficientes de correlación, incluidos el rango de Spearman y el coeficiente de Pearson: -1 ≤ r ≤ +1.
Cuándo usar cada método de cálculo
Los dos métodos descritos anteriormente se utilizarán de acuerdo con si hay parámetros asociados con los datos recopilados. Los dos términos a tener en cuenta son:
Mira También Qué Es El Reglamento Interno De Trabajo Y Qué Debe Contener
Qué Es El Reglamento Interno De Trabajo Y Qué Debe Contener- Paramétrico: Coeficiente de Pearson. Donde los datos deben ser manejados en relación a los parámetros de poblaciones o distribuciones de probabilidad. Normalmente se utiliza con datos cuantitativos ya establecidos dentro de dichos parámetros.
- No paramétrico: Rango de Spearman. Donde no se pueden hacer suposiciones sobre la distribución de probabilidad. Normalmente se usa con datos cualitativos, pero se puede usar con datos cuantitativos si el rango de Spearman resulta inadecuado.
En los casos en que ambos sean aplicables, los estadísticos recomiendan utilizar métodos paramétricos como el Coeficiente de Pearson, porque tienden a ser más precisos. Pero eso no significa descartar los métodos no paramétricos si no hay suficientes datos o si se necesita un resultado preciso más específico.
Interpretación de resultados
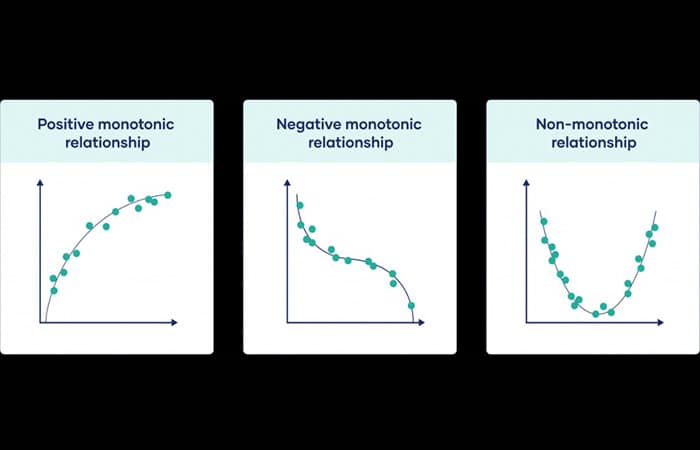
Por lo general, la mejor manera de obtener una interpretación generalizada pero más inmediata de los resultados de un conjunto de datos es visualizarlos en un gráfico de dispersión como estos:
Correlación positiva
Cualquier puntaje de +0.5 a +1 indica una correlación positiva muy fuerte, lo que significa que ambos aumentan al mismo tiempo. La línea de mejor ajuste, o línea de tendencia, es el lugar para representar mejor los datos en el gráfico. En este caso, está siguiendo los puntos de datos hacia arriba para indicar la correlación positiva.
Correlación negativa
Cualquier puntuación de -0,5 a -1 indica una fuerte correlación negativa, lo que significa que a medida que aumenta una variable, la otra disminuye proporcionalmente. La línea de mejor ajuste se puede ver aquí para indicar la correlación negativa. En estos casos tendrá una pendiente descendente desde el punto de origen.
Mira También VPN (Valor Presente Neto) – Fórmula, Significado y Calculadora
VPN (Valor Presente Neto) – Fórmula, Significado y CalculadoraSin correlación
Muy simple, una puntuación de 0 indica que no hay correlación o relación entre las dos variables. Cuanto mayor sea el tamaño de la muestra, más preciso será el resultado. No importa qué fórmula se utilice, este hecho será válido para todos. Cuantos más datos se introduzcan en la fórmula, más preciso será el resultado final.
Los valores atípicos o anomalías deben tenerse en cuenta en ambos coeficientes de correlación. El uso de un gráfico de dispersión es la forma más fácil de identificar cualquier anomalía que pueda haber ocurrido, y ejecutar el análisis de correlación dos veces (con y sin anomalías) es una excelente manera de evaluar la fuerza de la influencia de las anomalías en el análisis.
Si hay anomalías, se puede usar el coeficiente de rango de Spearman en lugar del coeficiente de Pearson, ya que esta fórmula es extremadamente robusta contra las anomalías debido al sistema de clasificación utilizado.
Correlación ≠ Causalidad
Si bien una relación significativa puede identificarse mediante técnicas de análisis de correlación, la correlación no implica causalidad. La causa no puede ser determinada por el análisis, ni debe intentarse esta conclusión. La relación significativa implica que hay más que entender y que hay factores extraños o subyacentes que deben explorarse más a fondo para buscar una causa.
Si bien es posible que exista una relación causal, sería negligente por parte de cualquier investigador utilizar los resultados de la correlación como prueba de esta existencia. Correlación no significa causalidad; sin embargo, un buen investigador sabe que las aplicaciones de los conocimientos estadísticos basados en correlación son infinitas si se obtienen los datos correctos.
Mira También Contabilidad Global. Qué Es, Historia, Desarrollo, Normas Y Más
Contabilidad Global. Qué Es, Historia, Desarrollo, Normas Y MásLa causa de cualquier relación que pueda descubrirse a través del análisis de correlación, es para que el investigador la determine a través de otros medios de análisis estadístico, como el análisis del coeficiente de determinación. Sin embargo, hay una gran cantidad de valor que puede proporcionar el análisis de correlación; por ejemplo, se puede estimar el valor de la dependencia o de las variables, lo que puede ayudar a las empresas a estimar el costo y la venta de un producto o servicio.
En esencia, los usos y aplicaciones de los análisis estadísticos basados en correlaciones permiten a los investigadores identificar qué aspectos y variables dependen unos de otros, cuyo resultado puede generar conocimientos procesables tal como son, o puntos de partida para futuras investigaciones y conocimientos más profundos.
Comparación de estudios
Un coeficiente de correlación también es una medida del tamaño del efecto, que indica la importancia práctica de un resultado. Los coeficientes de correlación no tienen unidades, lo que permite comparar directamente los coeficientes entre estudios.
Tal vez quieras conocer: Muestreo Sistemático. Qué Es, Tipos Y 7 Ventajas Y Desventajas
Usando un coeficiente de correlación
En la investigación correlacional se investiga si los cambios en una variable están asociados con cambios en otras variables.
Ejemplo de investigación correlacional
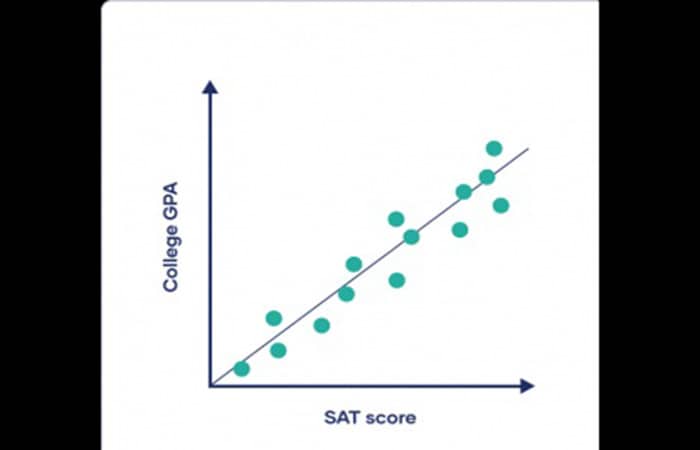
Investigas si los puntajes estandarizados de la escuela secundaria están relacionados con las calificaciones académicas en la universidad. Se predice que hay una correlación positiva: los puntajes más altos en el SAT se asocian con un GPA universitario más alto, mientras que los puntajes más bajos en el SAT se asocian con un GPA universitario más bajo.
Mira También Balance General. Qué Es, Elementos E Importancia
Balance General. Qué Es, Elementos E ImportanciaDespués de la recopilación de datos, puedes visualizar tus datos con un diagrama de dispersión trazando una variable en el eje x y la otra en el eje y. No importa qué variable coloques en cada eje. Inspecciona visualmente su gráfico en busca de un patrón y decide si hay un patrón lineal o no lineal entre las variables involucradas. El patrón lineal quiere decir que se puede ajustar una línea recta entre los puntos de datos, mientras que un patrón no lineal o con forma de curva, puede tomar formas diferentes, como una “U” o una línea con una curva.
Ejemplo de inspección visual
Reúne una muestra de 5000 graduados universitarios y los encuestas sobre sus puntajes SAT de la escuela secundaria y GPA universitarios. Visualiza los datos en un diagrama de dispersión para verificar un patrón lineal:
Hay muchos coeficientes de correlación diferentes que puedes calcular. Después de eliminar los valores atípicos, selecciona un coeficiente de correlación que sea adecuado en función de la forma general del patrón del gráfico de dispersión. Luego puedes realizar un análisis de correlación para encontrar el coeficiente de correlación de tus datos. Calcula un coeficiente de correlación para resumir la relación entre las variables sin sacar ninguna conclusión sobre la causalidad.
Ejemplo de análisis de correlación
Verifica si los datos cumplen con todos los supuestos para la prueba de correlación r de Pearson. Ambas variables son cuantitativas y se distribuyen normalmente sin valores atípicos, por lo que calcula el coeficiente de correlación r de Pearson. El coeficiente de correlación es fuerte en .58.
Interpretar un coeficiente de correlación
El valor del coeficiente de correlación siempre oscila entre 1 y -1, y lo tratas como un indicador general de la fuerza de la relación entre variables. El signo del coeficiente refleja si las variables cambian en la misma dirección o en direcciones opuestas: un valor positivo significa que las variables cambian juntas en la misma dirección, mientras que un valor negativo significa que cambian juntas en direcciones opuestas.
Mira También 10 Principios De Contabilidad: Historia, Normas Y Estándares
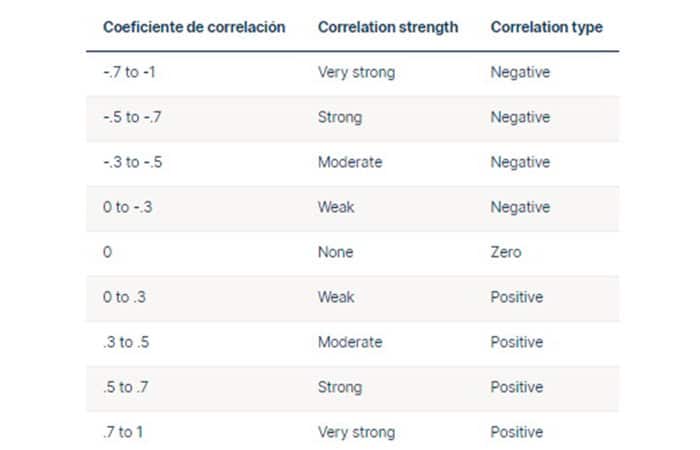
10 Principios De Contabilidad: Historia, Normas Y EstándaresEl valor absoluto de un número es igual al número sin su signo. El valor absoluto de un coeficiente de correlación describe la magnitud de la correlación: mientras mayor sea el valor absoluto, la correlación será más fuerte. Hay muchas pautas diferentes para interpretar el coeficiente de correlación porque los hallazgos pueden variar mucho entre los campos de estudio. Puedes utilizar la siguiente tabla como guía general para interpretar la intensidad de la correlación a partir del valor del coeficiente de correlación.
Si bien esta guía es útil en caso de apuros, es mucho más importante tener en cuenta el contexto y el propósito de tu investigación al formar conclusiones. Por ejemplo, si la mayoría de los estudios en tu campo tienen coeficientes de correlación cercanos a .9, un coeficiente de correlación de .58 puede ser bajo en ese contexto.
Visualización de correlaciones lineales
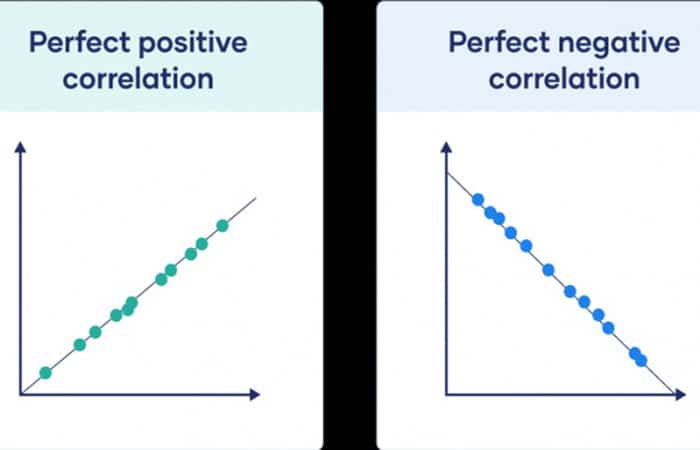
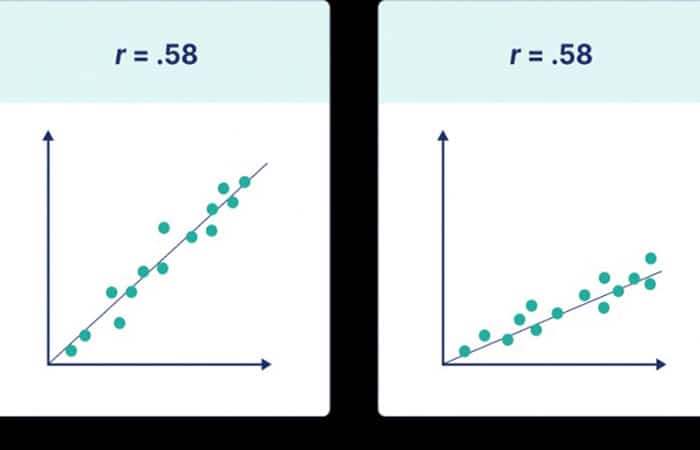
El coeficiente de correlación te dice qué tan cerca se ajustan tus datos en una línea. Si tienes una relación lineal, dibujarás una línea recta de mejor ajuste que tenga en cuenta todos los puntos de datos en un gráfico de dispersión. Cuanto más cerca estén los puntos de esta línea, mayor será el valor absoluto del coeficiente de correlación y más fuerte será la correlación lineal. Si todos los puntos están perfectamente en esta línea, tienes una correlación perfecta.
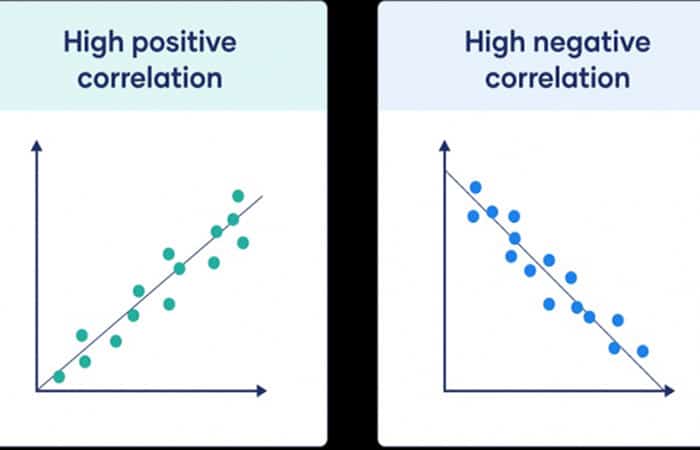
Si todos los puntos están cerca de esta línea, el valor absoluto de tu coeficiente de correlación es alto.
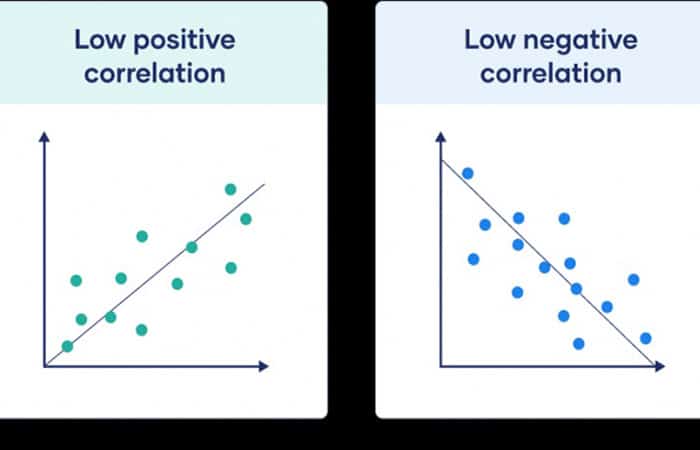
Si estos puntos se extienden lejos de esta línea, el valor absoluto de tu coeficiente de correlación es bajo.
Ten en cuenta que la inclinación o pendiente de la línea no se relaciona con el valor del coeficiente de correlación. Este coeficiente no te ayuda a predecir cuánto cambiará una variable en función de un cambio dado en la otra, porque dos conjuntos de datos con el mismo valor de coeficiente de correlación pueden tener líneas con pendientes muy diferentes.
Otros coeficientes
El coeficiente de correlación está relacionado con otros dos coeficientes, y estos te brindan más información sobre la relación entre las variables.
Coeficiente de determinación
Cuando elevas al cuadrado el coeficiente de correlación, obtienes la correlación de determinación (r2). Esta es la proporción de varianza común entre las variables. El coeficiente de determinación siempre está entre 0 y 1 y, a menudo, se expresa como un porcentaje.
r2: el coeficiente de correlación multiplicado por sí mismo.
El coeficiente de determinación se usa en modelos de regresión para medir cuánto de la varianza de una variable se explica por la varianza de la otra variable. Un análisis de regresión te ayuda a encontrar la ecuación para la línea de mejor ajuste y puedes usarlo para predecir el valor de una variable dado el valor de la otra variable.
Un alto r2 significa que una gran cantidad de variabilidad en una variable está determinada por su relación con la otra variable. Un r2 bajo significa que solo una pequeña parte de la variabilidad de una variable se explica por su relación con la otra variable; es más probable que las relaciones con otras variables expliquen la varianza de la variable.
El coeficiente de correlación a menudo puede sobrestimar la relación entre variables, especialmente en muestras pequeñas, por lo que el coeficiente de determinación suele ser un mejor indicador de la relación.
Coeficiente de alienación
Cuando quitas el coeficiente de determinación de la unidad (uno), obtienes el coeficiente de alienación. Esta es la proporción de varianza común no compartida entre las variables, la varianza no explicada entre las variables.
1 – r2 : uno menos el coeficiente de determinación
Un alto coeficiente de alienación indica que las dos variables comparten muy poca varianza en común. Un coeficiente de alienación bajo significa que la relación entre las variables explica una gran cantidad de varianza.
Preguntas frecuentes sobre los coeficientes de correlación
A continuación responderemos a algunas de las dudas y preguntas frecuentes relacionadas con el análisis de correlación:
¿Qué es una correlación?
Una correlación refleja la fuerza y/o dirección de la asociación entre dos o más variables.
- La correlación positiva significa que ambas variables cambian en la misma dirección.
- Una correlación negativa significa que las variables cambian en direcciones opuestas.
- La correlación cero significa que no hay relación entre las variables.
¿Cuántas variables hay en una correlación?
Una correlación generalmente se prueba para dos variables a la vez, pero puedes probar correlaciones entre tres o más variables.
¿Qué es un coeficiente de correlación?
Un coeficiente de correlación es un número único que describe la fuerza y la dirección de la relación entre las variables. Diferentes tipos de coeficientes de correlación pueden ser apropiados para tus datos en función de tus niveles de medición y distribución. El coeficiente de correlación producto-momento de Pearson (r de Pearson) se usa comúnmente para evaluar una relación lineal entre dos variables cuantitativas.
¿Cuáles son los supuestos del coeficiente de correlación de Pearson?
Estos son los supuestos que deben cumplir tus datos si deseas utilizar la r de Pearson:
- Ambas variables están en un nivel de medición de intervalo o razón.
- Los datos de ambas variables siguen distribuciones normales.
- Tus datos no tienen valores atípicos.
- Tus datos provienen de una muestra aleatoria o representativa.
- Esperas una relación lineal entre las dos variables.
¿Qué te dicen el signo y el valor del coeficiente de correlación?
Los coeficientes de correlación siempre oscilan entre -1 y 1. El signo del coeficiente indica la dirección de la relación: un valor positivo significa que las variables cambian juntas en la misma dirección, mientras que un valor negativo significa que cambian juntas en direcciones opuestas. El valor absoluto de un número es igual al número sin su signo. El valor absoluto de un coeficiente de correlación le indica la magnitud de la correlación: cuanto mayor sea el valor absoluto, más fuerte será la correlación.
¿Es el coeficiente de correlación lo mismo que la pendiente de la recta?
No, la inclinación o pendiente de la línea no está relacionada con el valor del coeficiente de correlación. El coeficiente de correlación solo te indica qué tan cerca se ajustan tus datos en una línea, por lo que dos conjuntos de datos con el mismo coeficiente de correlación pueden tener pendientes muy diferentes. Para encontrar la pendiente de la línea, deberás realizar un análisis de regresión.
Echa un vistazo a: Cómo Calcular La Tasa De Inflación: Fórmula Y Ejemplos
Pensamientos finales
El análisis de correlación en la investigación es un método estadístico utilizado para medir la fuerza de la relación lineal entre dos variables y calcular su asociación. En pocas palabras, el análisis de correlación calcula el nivel de cambio en una variable debido al cambio en la otra.
Una alta correlación apunta a una fuerte relación entre las dos variables, mientras que una baja correlación significa que las variables están débilmente relacionadas. Cuando se trata de investigación de mercado, los investigadores utilizan el análisis de correlación para analizar los datos cuantitativos recopilados a través de métodos de investigación como encuestas y sondeos en vivo.
Intentan identificar la relación, los patrones, las conexiones significativas y las tendencias entre dos variables o conjuntos de datos. Existe una correlación positiva entre dos variables cuando un aumento en una variable conduce al aumento en la otra. Por otro lado, una correlación negativa significa que cuando una variable aumenta, la otra disminuye y viceversa.
Deja una respuesta


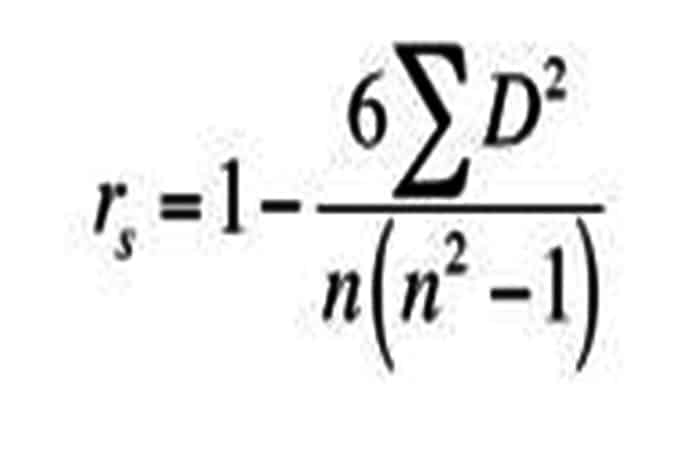
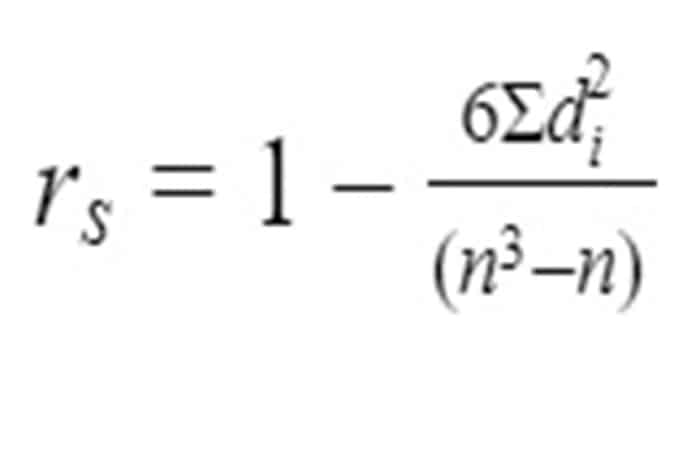
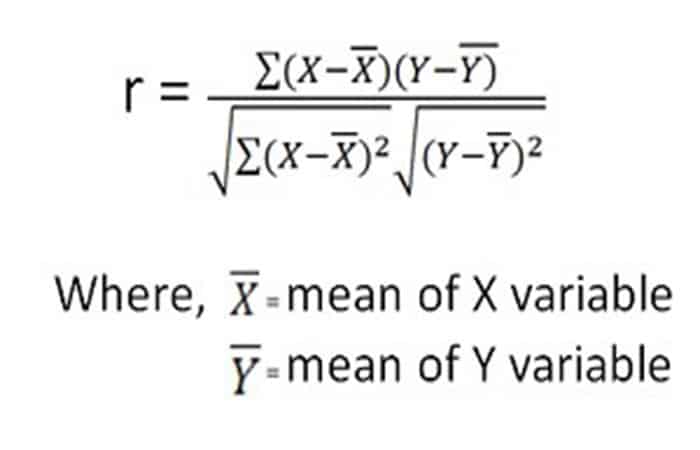



►TAMBIÉN DEBERÍAS LEER...