Gráfico De Control - Definición Y Explicaciones

¿Quieres saber qué es una tarjeta de control? Una tarjeta de control es una herramienta para determinar cuándo aparece la causa asignable que conduce a la deriva. Así, el proceso se detendrá en el momento adecuado, es decir antes de que produzca piezas no conformes (fuera del rango de Tolerancia).

Las tarjetas de control más utilizadas son las tablas de control de medidas de la media y el rango. Estos mapas se dibujan juntos e interpretaron juntos. De hecho, la distribución de dimensiones fabricadas modelada por una ley normal se caracteriza por la media y la dispersión (desviación estándar).

SPC y control de calidad

El creador de la tarjeta de control es Walter A. Shewhart, quien trabajó en el Laboratorio de Teléfonos Bell de Western Electric. Shewart publicó en 1931 los principios de la variabilidad de un proceso que distingue entre variabilidad aleatoria natural y variabilidad accidental.

La variabilidad natural surge de 'causas comunes de dispersión' o 'perturbaciones normales' incrustadas en el proceso de fabricación 'bajo control'.

La variabilidad accidental se debe a 'causas especiales' ocasionales y no controladas (materias primas con características fluctuantes, máquinas mal ajustadas, diferentes horarios de trabajo, calificación de la mano de obra, cambios de temperatura o presión, mala lubricación...).

El papel de SPC es determinar si el proceso está bajo control o no. Un análisis más detallado de las causas de las variaciones mejorará su desempeño y consistencia. Los cuadros de control son una herramienta gráfica para visualizar el proceso de fabricación a lo largo del tiempo y demostrar su estabilidad (seguimiento de causas especiales).

Mira TambiénQué Es La Departamentalización – Definición, Importancia Y Uso

La tarjeta de control

Permiten realizar un adecuado ajuste del proceso de fabricación y conocer la capacidad de la máquina. Esta herramienta se presenta como un gráfico cuyos puntos representan el seguimiento en el tiempo de una característica del proceso cuyo valor central (a menudo el promedio) está representado por una línea horizontal, así como los límites inferior (LCL) y superior (UCL). (UCL: Límite de control superior, LCL: Límite de control inferior).

Tal vez te puede interesar: Organizador Gráfico: Tipos Y Ejemplos En Línea Gratuitos

Estos dos valores son los límites dentro de los cuales el proceso está bajo control. Los valores de la característica controlada deben estar dentro de estos límites; de lo contrario, estos valores están "fuera de control" y deben examinarse.

Diferentes tipos de gráficos de control

Se necesitan dos gráficos de control para monitorear la posición y la dispersión.

Mira TambiénElementos Que Compone Un Membrete Corporativo

Mapas de variables cuantitativas

Las variables cuantitativas son medidas continuas (peso, longitud, espesor, temperatura, diámetro, etc.). Se comprueba en el tarjeta de control de medias o en el gráfico de rangos que la característica estudiada será estable en el tiempo. El tamaño de la muestra es de 4 a 6.

Mapas de variables cualitativas

Para medir las variables cualitativas (% defectuoso, ¨% fallas, etc.), se utilizan mapas con atributos p, np oc para verificar los atributos a lo largo del tiempo. El tamaño de la muestra está en el rango de 50 a 100.

Tarjeta de control de media y amplitud

Estos dos parámetros son independientes y complementarios. El valor medio puede variar sin que varíe la dispersión y viceversa.

Estos gráficos de control permiten visualizar la evolución de la dispersión de las dimensiones fabricadas. La tarjeta de control de desviación estándar es "más justa” y menos dispersa que la tarjeta de control de tramo.

Por otro lado, los cálculos a realizar para trazar la gráfica de control del rango son menos complicados y por tanto más fiables. El tarjeta de control de desviación estándar se implementará si el diseño del gráfico está computarizado o asistido por una herramienta de cálculo automático. La gráfica de control de la extensión se implementará si la traza de la gráfica de control es manual en un soporte de papel.

Objetivo

Esta tarjeta de control permite visualizar la evolución y la variación del valor medio de las dimensiones fabricadas. Esta tarjeta de control está trazada por puntos sucesivos que representan el valor medio de la muestra tomada a intervalos regulares.

Mira TambiénGestión Financiera: Roles Y Responsabilidades De Las Partes Interesadas

El objetivo es comparar el rendimiento medio de la producción a lo largo del tiempo utilizando un mapa que caracteriza la tendencia del valor central. Se realizan varias observaciones individuales en varios subgrupos numerados con una frecuencia de tiempo determinada (cada hora, tres veces al día, etc.).

En cada subgrupo cronológico k, se realizan n observaciones. El promedio del subgrupo se traza en el gráfico de promedios de acuerdo con su número cronológico que se trazará en el eje horizontal de los gráficos de control. Debido al teorema límite central, la media de los valores en la tarjeta de control sigue una distribución normal, independientemente de que las observaciones estén distribuidas normalmente o no.

Esta ley es válida incluso para muestras pequeñas, lo que es frecuente en el control de calidad. Se dirá que una producción es 'estable' si la tendencia y la dispersión son estadísticamente constantes en el tiempo. La tarjeta de control promedio monitorea la configuración del proceso, la tarjeta de rango monitorea las dispersiones.

Límites de control

Ahora, veamos los límites de control

La desviación estándar es conocida

El cálculo de los límites del mapa de medias difiere según se conozca o no la desviación estándar. Cuando se conoce la desviación estándar del proceso, las características de la distribución normal permiten calcular los límites de control. El intervalo [ μ - 3σ; - μ + 3σ ], contiene el 99,7% de los datos y representa los límites LCL y UCL de los gráficos de control.

Por tanto, la probabilidad de que un punto esté fuera de los límites es del 0,3%. El valor de la media difiere significativamente según se conozca o no la desviación estándar de la población. Si se desconoce el valor real de la media µ de las observaciones, se puede reemplazar por la media por muestra.

Mira TambiénDeflactor Del PIB - Qué Es, Definición Y Concepto

El 94,74% de los puntos debe estar entre los límites si el proceso está bajo control. La interpretación del mapa de medias es la misma tanto si se conoce como si se desconoce el media real del proceso.

La desviación estándar es desconocida.

En muchos casos, la desviación estándar σ se desconoce y debe estimarse mediante t (ley de Student) en lugar de la distribución normal estándar. Luego usamos un coeficiente A2 que depende del número de observaciones en cada muestra y del tipo de mapa utilizado. Los límites de control se estiman utilizando el rango medio de observaciones dentro de un subgrupo como medida de variabilidad.

Con:: rango medio en la muestra.

Es igual a la media de los rangos (valor máximo del subgrupo - valor mínimo) de cada subgrupo. Los límites se estrechan a medida que aumenta el tamaño del subgrupo de la muestra.

Un ejemplo

La empresa Emballex fabrica cajas metálicas cuyo peso se controla al final de la producción. Esta característica depende esencialmente de la composición de las materias primas y de la calidad de la aleación producida.

La empresa decide controlar el proceso de fabricación mediante tarjetas de control para el peso medio de las piezas y el rango de peso de cada muestra tomada. El control consiste en sacar 5 cajas de la máquina y pesar cada caja. El peso expresado en gramos. Los pesos se registraron en una serie de 20 muestras tomadas.

Trace los gráficos de control para los gráficos X y R.

Exh no.	X1	X2	X3	X4	X5	Promedio	Verano
1	81	85	82	84	83	83	4
2	86	81	83	84	80	82	6
3	87	87	87	88	82	86,2	5
4	87	85	89	86	84	85,2	6
5	81	89	86	85	87	85,6	8
6	84	81	87	87	84	84,6	6
7	84	87	93	87	85	87,2	9
8	87	86	82	87	86	85,6	5
9	83	79	87	84	86	83,8	8
10	85	82	85	84	86	84,4	4
11	81	83	85	85	84	83,6	4
12	85	79	78	83	86	82,2	8
13	87	83	89	85	80	84,8	9
14	87	86	86	79	83	84,2	8
15	89	82	86	86	85	85,6	7
dieciséis	90	84	81	85	83	84,6	9
17	86	82	85	86	88	85,4	6
18	85	83	83	85	89	85	6
19	80	81	83	87	82	82,6	7
20	85	89	82	79	83	85,6	10

• El peso medio es de 84,5 g.
• El límite superior es 87,81 g.
• El límite inferior es 81,18 g.
• El proceso de fabricación está bajo control.

Mapa en la medida

Gráficos de control de extensión: Este tarjeta de control se utiliza para visualizar la evolución y variación de la extensión (imagen de la dispersión) de las dimensiones fabricadas. Esta tarjeta de control se dibuja mediante puntos sucesivos que representan la cantidad de muestras tomadas a intervalos regulares.

con :: rango medio en la muestra = R1 + R2 + ... + Rk / k.

Ri extensión del subgrupo i. k: número de subgrupos. La media de los rangos indica la importancia de la variabilidad natural del proceso.

Para el ejemplo anterior, la amplitud promedio es de 6.750 g.

• El límite inferior es: 0 g.
• El límite superior es: 14,28 g.
• El proceso de fabricación está bajo control.

Coeficientes

Estos coeficientes se utilizan para calcular los límites de control según el tamaño de la muestra y el tipo de tarjeta utilizada.

Tamaño	A2	D3	D4	Sigma
2	1.880	0	3,267	1.128
3	1.023	0	2.575	1,693
4	0,729	0	2.282	2.059
5	0.577	0	2.115	2.326
6	0.483	0	2.004	2.534
7	0,419	0.076	1,924	2.707
8	0.373	0,136	1.864	2.847
9	0.337	0,184	1.816	2,970
10	0.308	0,223	1,777	3.078
11	0,285	0,256	1.744	3,173
12	0,266	0,284	1.716	3258
13	0,249	0.308	1,692	3.336
14	0,235	0.329	1,671	3.407
15	0,223	0.348	1,652	3.472
dieciséis	0,212	0.364	1.636	3.532
17	0,203	0.379	1.621	3.588
18	0,194	0.392	1,608	3.640
19	0,187	0.404	1,596	3.689
20	0,180	0,414	1,586	3.735

Gráficos de control de atributos

Si no se desea realizar un control de variables por medidas, o si esto no es posible, se preferirá el control de calidad por atributos que consiste en señalar la presencia o ausencia de un criterio cualitativo sobre las partes controladas.

Ejemplos: inspección visual (ausencia de avería o no), dimensión demasiado pequeña o demasiado grande (paso de la pieza por un calibre)...

Las principales tarjetas de control de atributos son:

• La tarjeta p para la proporción de defectuosos.
• La tarjeta np para controlar el número de artículos defectuosos
• La tarjeta c para monitorear el número de fallas.

Tarjeta p

Ahora veamos las características de este tipo de grafico de control

Principio

Este mapa se utiliza para monitorear la proporción p de productos defectuosos contenidos en una muestra proveniente de un lote o de una máquina. En un muestreo aleatorio, a intervalos regulares, de una muestra de n partes, observamos el número de defectuosas encontradas que dividimos por el tamaño de la muestra n (n> 50) para obtener p.

• p = número de piezas defectuosas / número de piezas en la muestra = d / n

P se traza periódicamente en un tarjeta de control donde se muestra la proporción promedio de defectuosos y los límites superior e inferior correspondientes.

Los límites de control se ubican en 3 desviaciones estándar a cada lado de la proporción promedio.

• La ley que gobierna la gráfica de control p es la ley binomial: observación de d partes defectuosas (dos métodos) en una muestra aleatoria de n partes. Cuando n es grande, una aproximación por la distribución normal es legítima. El intervalo [ μ - 3σ; - μ + 3σ], entonces contiene el 99,7% de los datos contenidos en los límites LCL y UCL de los gráficos de control.

Ejemplo

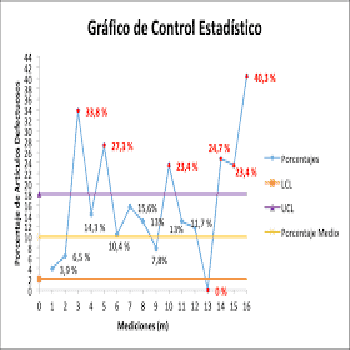
GLASSEX fabrica mangos de plástico utilizados en muebles de cocina y baño. Se realiza un control visual cada hora sobre una muestra de 65 mangos para detectar los principales defectos: rayones, color dudoso, microgrietas, etc. con el fin de controlar la tasa de defectos en el proceso de fabricación. Los resultados de 28 series de muestras se dan en la tabla de al lado.

Se obtiene un promedio para p de 0.079 con una desviación estándar promedio de 0.031 de defectuoso.

El límite superior de la tarjeta p es 0,179.

Tarjeta np

Se recomienda el uso de la tarjeta np si el tamaño de muestra n sigue siendo el mismo para cada serie de muestras. El número de artículos defectuosos observados cronológicamente en las muestras sucesivas se traza en la tarjeta np. El número de defectuosos en una muestra de tamaño n es d = np. Para k muestras n, el número promedio de defectuosos.

Podemos calcular los límites de control basados ​​en intervalos de tres desviaciones estándar alrededor del número promedio de defectuosos.

Tarjeta c

La tarjeta c se utiliza para seguir cronológicamente el número de averías por unidad comprobada (100 metros de cable, 20 metros de rollo de papel tapiz,...). Se diferencia de las tarjetas p y np, porque el criterio que se sigue es el número de defectos y no el número de defectuosos (rechazados), parte que presenta defectos que pueden ser aceptados o no. Dependiendo del criterio de gravedad del defecto (crítico, mayor o menor), la pieza se considerará defectuosa o no. El número promedio de fallas observadas en k unidades

Verificadas es:

c i es el número de fallas observadas para la i-ésima unidad verificada.

Aquí puedes aprender sobre: 5 Organizadores Gráficos: Cuándo, Cómo Y Para Qué Usarlos

Conclusión

Como puedes ver, un tarjeta de control ayuda a producir piezas no conformes (fuera del rango de Tolerancia) para el seguimiento en el tiempo de una característica del proceso cuyo valor central (a menudo el promedio). Es bueno implementar estos tipos de gráficos para agilizar tus procesos. Esperamos haberte ayudado con esta información .