La Función De Producción. Descripción, Teorías Y Cálculo

En este artículo te hablaremos de la función de producción. Las funciones de producción Cobb-Douglas que involucran tecnología específica del sector o productividad multifactorial (TEFF), capital (KS) y mano de obra (LABS) proporcionan valor agregado potencial (VADDP) en cada sector, teniendo en cuenta el nivel de utilización de la capacidad (CAPUT), inicialmente fijado exógenamente.

En un modelo multisectorial, las funciones requieren exponentes sectoriales para el capital (CDALFS) y el trabajo que, asumiendo rendimientos constantes a escala, suman uno dentro de los sectores.

Solow (1956) reconoció hace mucho tiempo que la función de producción Cobb-Douglas estándar con un coeficiente de escala constante frente a los términos de capital y trabajo era inadecuada porque la expansión del stock de capital y la oferta de trabajo deja una gran parte del crecimiento económico sin explicar.

Entonces se convirtió en una práctica estándar representar un término de crecimiento de tecnología especificado exógenamente frente a los términos de capital y trabajo como progreso tecnológico "incorpóreo".

Quizás te puede interesar: Ingeniería En Producción. Que Es, Cuanto Dura, Donde Se Puede Hacer

Mira TambiénRequisitos para renovar un crédito Fonacot

Función de producción

Romer (1994) comenzó a mostrar el valor de desempaquetar dicho término y especificar sus elementos en el modelo, representando así de manera endógena este residuo por lo demás muy grande, que podemos entender que representa el crecimiento de la productividad multifactorial (MFP).

En los IF, ese factor de crecimiento de la productividad endógena total (TEFF) es la acumulación a lo largo del tiempo (por lo tanto, un stock como trabajo y capital) de valores anuales de crecimiento en la productividad multifactorial (MFPGRO).

Hay muchos componentes que contribuyen al crecimiento de la productividad y existe una vasta literatura sobre ellos. En el desarrollo de los FI hubo una elección filosófica fundamental que tomar. Una opción era mantener la función de productividad de múltiples factores muy simple, quizás restringirla a uno o dos impulsores clave, y estimar la función con el mayor cuidado posible.

Las sugerencias incluyeron centrarse en la disponibilidad / precio de la energía y el crecimiento de las redes electrónicas y la sociedad del conocimiento. La segunda opción fue desarrollar una función que incluyera muchos más factores conocidos o fuertemente sospechados que influyen en la productividad e intentar una representación más estilística de la función, utilizando la investigación empírica para ayudar al esfuerzo tanto como sea posible.

Ventajas y desventajas

Las ventajas del segundo enfoque incluyen la creación de un modelo que responda mucho más a una amplia gama de palancas políticas a largo plazo. Las desventajas incluyen algunas complicaciones inevitables con respecto a la superposición y la redundancia de la representación de los factores, así como una considerable complejidad de presentación.

Debido a que los IF son una herramienta de pensamiento y un sistema multimodelo ampliamente integrado, se adoptó el segundo enfoque y la función de producción se ha convertido en un elemento del modelo económico que estará sujeto a revisiones y mejoras periódicas. Los IF agrupan los muchos impulsores de la productividad multifactorial en cinco categorías, reconociendo que incluso las categorías se superponen un poco.

Mira TambiénRequisitos para Crédito Fonacot por primera vez

La categoría base es aquella que representa el desarrollo tecnológico central y los elementos de transferencia de la teoría de la convergencia, y los países menos desarrollados están alcanzando gradualmente a los más desarrollados. Las otras cuatro categorías incorporan factores que pueden retardar o acelerar dicha convergencia, transformando la formulación general en una de convergencia condicional.

La base de convergencia

La tasa base de crecimiento de la productividad multifactorial (MFPRATE) es la suma de la tasa de crecimiento para el avance tecnológico o la creación de conocimiento de un líder tecnológico en el sistema global (mfpleadr) y una prima de convergencia (MFPPrem) que es específica para cada país / región.

El concepto básico es que puede ser más fácil para los países menos desarrollados adoptar la tecnología existente que para los países líderes desarrollarla (asumiendo que se ha cruzado algún umbral básico de desarrollo).

La tasa base para el líder sigue siendo un residuo inexplicable en la representación endógena de MFP, pero tiene el valor de ponerla a disposición de los usuarios del modelo para representar, si lo desean, ciclos tecnológicos a lo largo del tiempo (por ejemplo, ondas de Kondratief).

La base también incluye un término de corrección (MFPCor) que se establece inicialmente a la diferencia entre el crecimiento empírico de MFP (calculado el primer año como un residuo entre el crecimiento de los factores y el crecimiento de la producción) y la suma de los términos de líder tecnológico y prima de convergencia.

Tiempo extraordinario, el término de corrección se elimina gradualmente, pero los otros cuatro términos (a continuación) se convierten en impulsores clave de la productividad específica del país. De hecho, un cambio significativo en los otros términos puede socavar el proceso de convergencia fundamental o aumentarlo en gran medida.

Mira TambiénCómo Saber si Tengo DICOM

Capital humano

Este término tiene múltiples componentes, incluidos los cambios en el gasto en educación como parte del PIB, el nivel educativo de los adultos y los cambios en el gasto en salud. Por ejemplo, Barro y Sala-i-Martin (1999: 433) estimaron que un aumento de 1,5% en el gasto público en educación se traduce en aproximadamente un 0,3% de aumento en el crecimiento económico anual.

Capital social

De manera similar, la representación del capital social agrega varios componentes, incluida la libertad económica y la ausencia de conflicto social manifiesto. De manera ilustrativa, el valor del parámetro de libertad económica se estimó en una relación transversal del cambio en el nivel del PIB de 1985 a 1995 con el nivel de libertad económica. Del mismo modo, Barro pone gran énfasis en su trabajo de estimación sobre el "estado de derecho".

Capital físico

En un trabajo colaborativo con el proyecto IFs, Robert Ayres enfatizó correctamente la estrecha relación entre la disponibilidad de suministro de energía y el crecimiento económico. Por ejemplo, un rápido aumento de los precios mundiales de la energía (WEP) esencialmente hace que gran parte del capital social sea menos valioso.

Los IF utilizan el precio mundial de la energía en relación con los precios mundiales de la energía del año anterior para calcular un término de precio de la energía. El término capital físico también representa el alcance de varios tipos de infraestructura en una sociedad.

Capital del conocimiento

Este cuarto término incluye cambios en el gasto en I + D, calculado a partir del gasto público (GDS) en I + D como parte del gasto público total (GOVCON) que contribuye a la creación de conocimiento, especialmente en los países más desarrollados. Globerman (2000) revisó el trabajo empírico sobre los retornos privados y sociales del gasto en I + D y los encontró en el rango del 30-40%.

Sin duda, muchos otros factores contribuyen a una difusión superior del desarrollo del conocimiento. Este término representa especialmente el grado de integración económica con la economía global a través del comercio.

Mira TambiénCómo Solicitar Un Crédito Fonacot para Damnificados

Todos los elementos calculados en términos de capital humano, social, físico y de conocimiento se utilizan para configurar la productividad económica y las tasas de crecimiento del modelo sobre una base diferencial, es decir, se calculan y evalúan en relación con los patrones "esperados" subyacentes dados en general, niveles de desarrollo económico.

Sus niveles reales pueden estar por encima o por debajo de los esperados y, por lo tanto, pueden aumentar o ralentizar la tasa de crecimiento de la productividad.

El enfoque de la función de producción. Cálculo

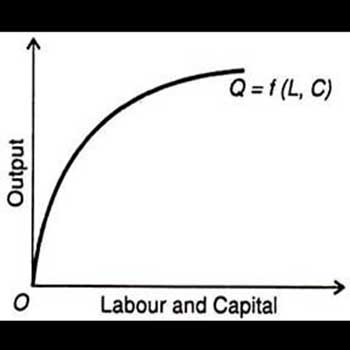
La función de producción es una expresión matemática abreviada para un proceso de entrada-salida. Su uso fue motivado principalmente por un intento de dar cuenta de la forma en que crecen las economías. Es la base de la teoría moderna del crecimiento y de la contabilidad del crecimiento, del intento de responder a la pregunta; ¿Qué factores explican el crecimiento observado en la economía y en qué medida?

Como tal, también responde a la pregunta: ¿qué explica las ganancias de los diversos insumos y sus propietarios? La producción total Q se ve que como resultado invariablemente e inexorable de la aplicación de entradas de agregado K y N. Los tres se han identificado con varios agregados estadísticos. El tratamiento clásico es el artículo fundamental de Solow.

(1) Q = A (t) f (K, N)

Donde el "factor multiplicativo A (t) mide el efecto acumulado de los cambios en el tiempo" (Solow 1956: 402). Los cambios en la función de producción a los que se hace referencia implican un "cambio técnico". Al igual que con las formulaciones asociadas a la teoría de Böhm-Bawerk, es posible dejarse llevar por los aspectos técnicos de la función de producción y dedicar tiempo a un examen detallado de sus diversas formas posibles (Cobb Douglas, CES, etc.) y sus implicaciones.

Mira También5 Mejores Programas De Contabilidad Para PYMES

Una forma más caritativa, y quizás más esclarecedora, de interpretar la literatura sobre la teoría del crecimiento es como "una invitación a una conversación". La conversación trata sobre la mejor manera de describir el "progreso económico". Esto está claro desde el principio. En la formulación anterior, Solow no puede explicar el crecimiento observado en la producción (medida) considerando las entradas de K y N (medidos) solo.

Como resultado, debes buscar otra cosa para explicar el "residual". En este caso es A (t) el parámetro "cambio técnico". Entonces el crecimiento es el resultado de insumos de capital, trabajo y progreso técnico. La conversación posterior trata básicamente sobre lo que esto significa y qué son realmente estas cosas (capital, trabajo y progreso técnico).

De hecho, la conversación se ha ampliado considerablemente en los últimos años con un resurgimiento de la teoría del crecimiento que se ha concentrado en estas cuestiones. Debido a que se ha convertido en una explicación del progreso técnico en términos de decisiones motivadas económicamente, en lugar de como un parámetro de cambio "exógeno" (inexplicable), se le ha llamado "teoría del crecimiento endógeno".

En el proceso, el significado y la naturaleza de la función de producción y sus argumentos (capital, trabajo y cambio técnico) han sido objeto de un examen más detenido. Podemos examinar esto más a fondo si observamos más de cerca las implicaciones del enfoque de la función de producción.

Rendimientos constantes a escala y teoría del crecimiento endógeno

Esencialmente, la función de producción describe un proceso de transformación física de insumos en productos. Para que tenga algún uso práctico se debe indicar la forma de esta transformación. Es decir, debe poder especificar cómo varía la salida en respuesta a cambios en las entradas. Aquí viene a la mente la noción de rendimientos constantes a escala (CRS).

Parece lógico que si se duplicaran todas las entradas relevantes, la salida debería, como resultado, duplicarse. Y si CRS prevalece, entonces se deduce que los retornos a cualquier factor de entrada que pueda variarse continuamente, mientras que los demás se mantienen constantes, disminuirán.

Mira TambiénEl Origen De La Contabilidad Y Su Evolución Histórica

Por tanto, las ganancias de los insumos de los factores (y, por implicación, de sus propietarios) pueden explicarse asumiendo que se les paga en términos del valor de sus productos marginales decrecientes. CRS se basa, como lo ha expresado Romer (1990: 98, 1994: 12), en la noción de replicación.

Si todas las entradas relevantes se identifican correctamente, entonces es posible, en principio, replicar (por lo tanto duplicar) el proceso. La premisa más básica de nuestro razonamiento científico sobre el mundo físico es que es posible replicar cualquier secuencia de eventos replicando las condiciones iniciales relevantes (Esto es tanto una declaración de fe como una definición de las condiciones relevantes).

¿Qué significa esto?

Para la teoría de la producción, esto significa que es posible duplicar la producción de cualquier proceso de producción duplicando todos los insumos. La noción de causalidad física (determinismo) está en la base misma de la teoría de la producción. Esta noción es, sin duda, como principio, indiscutible. Es casi didáctico.

Si todas las condiciones relevantes (incluidas las acciones individuales necesarias, después de decisiones conscientes) que dieron lugar a ("causaron") cualquier situación, fueran restablecidas de alguna manera, entonces la misma situación, casi por definición, volvería a surgir. Esto se considera cierto sin excepción, excepto por el paso del tiempo.

En las ciencias físicas, cuando se trata de eventos fácilmente verificables y clasificables (como la luna llena, el surgimiento de un producto homogéneo de una línea de producción), el número de condiciones relevantes (iniciales) es manejablemente pequeño. La reproducción, identificación o producción del "mismo" evento es, por tanto, bastante simple.

En las ciencias sociales, sin embargo, todo depende de identificar correctamente estas condiciones relevantes. Aunque los procesos físicos simples y bien entendidos, como algunos procesos de producción, se replican fácilmente, la transición de estos al nivel de economía agregada es extremadamente problemática.

Mira TambiénEl Mejor Software De Contabilidad Para Pequeñas Empresas

En el nivel más simple está el problema insuperable de la agregación de las diversas salidas y entradas y la correspondencia de los valores estadísticos agregados con los símbolos teóricos (supuestamente en términos puramente físicos). Sin embargo, como se indicó anteriormente, quizás no sea necesario tomar estas formulaciones tan literalmente.

Al considerar la función de producción como un dispositivo metafórico que invita a la conversación y la especulación, las consideraciones anteriores sugieren que la conversación trata sobre las "condiciones iniciales relevantes". Esto se puede ver (y ha quedado claro, por ejemplo, en la aplicación de la teoría del comercio internacional de Hecksher-Ohlin durante muchos años) al considerar la relación entre los factores de producción y el progreso técnico.

Ejemplo de cálculo

Considera una función de producción de CRS en tres argumentos, tierra, trabajo y capital (L, N y K), de modo que:

(2) Q = f (K, N , L ) yl Q = f ( l K , l N , l L )

Donde l es un escalar positivo. Llama a esto una función de producción completa. Es completo en el sentido de que incluye todos los insumos pertinentes y necesarios para la producción del producto. Para una función de producción completa es posible escribir:

(3) gQ = s 1 g K + s 2 g N + s 3 g L

Mira TambiénContabilidad Nacional. Qué Es, Significado E Importancia

Donde g indica la tasa proporcional de crecimiento del símbolo y s i (i = 1...3) es la "participación" del factor en (contribución a) el crecimiento de la producción gQ. Debe ser cierto que s1 + s2 + s3 = 1, por lo que las acciones de los factores agotan completamente el producto (según la ley de Euler si los factores se pagan según sus acciones, es decir, según sus productos marginales, sus las ganancias combinadas equivaldrían al producto total). Ahora, si uno omite por error uno de los argumentos, di land, L, y escribe la función

(4) Q = q (K , N )

Entonces esta función tendría rendimientos decrecientes a escala. Llama a esto una función de producción parcial. Es inconcebible que cualquier función de producción realmente observada (medida) no sea de alguna manera una función de producción parcial.

Cuando usamos una función de producción para hacer inferencias a partir de estadísticas observadas, sin duda esperamos que la función parcial que hemos postulado se comporte, en algunos aspectos cruciales, como una completa. Duplicar K y N sería menos del doble de Q ya que L no se duplica. Entonces no se tendría en cuenta algún "crecimiento". Si lo atribuimos a un parámetro de desplazamiento A (t), como en la función Solovian:

(5) Q = A (t) q (K, N),

Entonces parece como si el crecimiento fuera en parte debido a alguna causa "exógeno" (progreso técnico), cuando, de hecho, es debido a la productividad de L. El mismo ejercicio se puede aplicar a una situación en la que algunos de entrada, lo llaman H, actúa en la salida Q mediante la mejora de la productividad de N. Entonces una función completa:

(6) Q = f (K, N, H)

Que omite H, como en:

(4) Q = q (K, N)

Será "desplazado" por cambios "externos" en H. Una consideración relacionada es la cuestión de los insumos no rivales. Los insumos no rivales, de los que hay muchos ejemplos, "son insumos valiosos en la producción que pueden utilizarse simultáneamente en más de una actividad".

Los procesos químicos, el diseño de chips de computadora, un dibujo mecánico, una fórmula metalúrgica (u otra), software de computadora, entre otros, son ejemplos de insumos no rivales (ibid). Pueden ser excluibles (apropiables) o no. Si H es un conjunto de entradas no rivales y R es un conjunto de entradas rivales (como K, N), entonces:

(7) Q = f (H, R)

Tiene las propiedades que:

(8) f ( l H, l R)> f ( H, l R) = l f ( H, R )

Es decir, hay rendimientos crecientes a escala debido a los beneficios "externos" de la acumulación privada de H. La A (t) en la ecuación básica de Solow (1) anterior también puede entenderse como la expresión de insumos no rivales. Identificarlos y hablar de ellos los vuelve "endógenos".

Tal vez quieras saber: Punto De Equilibrio Financiero. Qué Es Y Cómo Se Calcula

Limitaciones del marco de la función de producción

Las limitaciones del marco de la función de producción están relacionadas con su existencia dentro de un mundo de equilibrio. Está en equilibrio en el sentido de que se supone que la función de producción representa el conocimiento que está disponible no solo para el teórico sino también, de alguna manera, para los agentes económicos del modelo.

Se supone que las salidas se derivan de una manera técnicamente conocida de la aplicación de los insumos y el valor de los productos también se conoce, de modo que a los insumos se les paga el valor de sus productos marginales. No hay lugar ni análisis de diferencias en las valoraciones individuales de insumos y productos.

No es suficiente suponer que las cosas solo se conocen "probabilísticamente", ya que esto supone que se conoce un número finito de resultados posibles y su distribución. No hay competencia "como proceso de descubrimiento". Los teóricos del crecimiento han intentado extender este enfoque inherentemente estático en un intento de incorporar el cambio tecnológico y la innovación.

Lo han hecho considerando la I + D, por ejemplo, como otra entrada (en parte no rival), como H, con un producto marginal medible conocido. En la medida en que la I + D conduzca al descubrimiento de técnicas y productos "nuevos", se trata de una contradicción de términos. No podemos tener conocimiento futuro en el presente.

Es posible que tengamos una expectativa general (basada en experiencias pasadas) o la esperanza de que los gastos en I + D den frutos, pero no podemos saber de antemano exactamente de qué manera. Si lo hiciéramos, los gastos de I + D serían innecesarios.

Si bien la "nueva economía del crecimiento" ha hecho mucho por traer estos importantes aspectos nuevamente al alcance de la economía, el marco de equilibrio tradicional que ha utilizado debe considerarse inadecuado para dar cuenta de estos importantes fenómenos.

¿Cuál es el enfoque de la función de producción?

El enfoque de la función de producción para el crecimiento equivale a señalar que ciertas cosas (insumos) estaban (históricamente) presentes y que podrían explicar la experiencia de crecimiento y posiblemente podrían presentarse de manera similar en el crecimiento futuro. Es un enfoque de caja negra en la medida en que no "explica" completamente la conexión, el proceso en el tiempo.

En particular, ignora cualquier factor "extraeconómico" como el entorno político e institucional o, más exactamente, estos están, en el mejor de los casos, implícitos en los análisis. (Sin embargo, para un intento de explicar explícitamente estos fenómenos mientras permanece dentro del marco de la función de producción).

La función de producción es una caja negra también en la medida en que subsume la toma de decisiones individual. Como ha señalado Kirzner: una función de producción puede considerarse "positivamente". Como tal, representa simplemente un conjunto de relaciones tecnológicas. Por otro lado, una función de producción puede considerarse como una representación de oportunidades, entre las cuales un ser humano puede elegir.

Claramente, una economía en la que los eventos del mercado se ven como el resultado de acciones deliberadamente planificadas, debería ver las posibilidades de producción, de esta segunda forma, como alternativas entre las cuales se pueden construir cursos de acción planificados.

La práctica actual en general (y, como nos parece, desafortunadamente) sigue la visión "tecnológica". Este es especialmente el caso con respecto a los modelos agregados. Esta práctica es especialmente desafortunada en el contexto de la teoría del capital.

Ejemplos de funciones de producción

A continuación te mostramos algunos ejemplos de función de producción:

Proporciones fijas

Una importante familia de tecnologías de modelos de funciones de producción que involucran una sola técnica de producción. La única forma de producir una unidad de producción, por ejemplo, puede ser utilizar 1 máquina y 2 trabajadores. Si la empresa tiene disponibles 2 máquinas y 2 trabajadores, la máquina adicional simplemente permanece inactiva, y si quiere producir dos unidades de producción, entonces tiene que usar 2 máquinas y 4 trabajadores. Tal función de producción tiene proporciones fijas.

¿Cómo podemos describir una tecnología así con precisión? Si la única forma de producir unidades de producción es utilizar máquinas y 2 y trabajadores, entonces la producción de z1 es máquinas y z2 es corresponde a los trabajadores. Esto es:

min {z1, z2 /2},

El mínimo de z1 y z2 / 2. Comprueba la lógica de esta fórmula considerando la salida que asigna a varias combinaciones de máquinas y trabajadores:

• 1 máquina y 2 trabajadores rinden min {1,2 / 2} = min {1,1} = 1 unidad de producción.
• 2 máquinas y 2 trabajadores rinden min {2,2 / 2} = min {2,1} = 1 unidad de producción.
• 2 máquinas y 4 trabajadores rinden min {2,4 / 2} = min {2,2} = 2 unidades de producción.

Una función de producción de proporciones fijas general para dos insumos tiene la forma:

min { a z 1 , b z 2 }

para algunas constantes a y b . La tecnología que modela esta función de producción implica una técnica única que produce una unidad de salida a partir de 1 / a unidades de entrada 1 y 1 / b unidades de entrada 2 y, más generalmente, y unidades de salida a partir de y / a unidades de entrada 1 y y/b unidades de entrada 2.

No se pueden utilizar unidades adicionales de ninguna de las entradas. Por ejemplo, si la empresa tiene y / a unidades de entrada 1 y más de y / b unidades de entrada 2 --- digamos z 2 unidades. Entonces su salida es: min {a (y / a), b z 2 } = min { y , b z 2 } = y , ya que z 2 > y / b.

Si hay más de dos insumos, una tecnología de técnica única puede modelarse mediante una función de producción con una forma similar. Por ejemplo, si se necesitan cuatro ruedas, un motor y un cuerpo para fabricar un automóvil, y no es posible la sustitución entre las entradas, el número de automóviles que se pueden producir a partir del vector (z1, z2, z 3) de entradas, donde la entrada 1 son ruedas, la entrada 2 son motores y la entrada 3 son cuerpos. Esto es:

min {z1/4, z2 , z3 }.

Sustitutos perfectos

Una tecnología cuyo carácter es exactamente opuesto al de una tecnología de proporciones fijas permite sustituir libremente un insumo por otro a un ritmo constante. Por ejemplo, se puede hacer una hamburguesa con 100 g de carne de res canadiense, o con 50 g de carne de res canadiense y 50 g de carne de res de otro tipo, o cualquier combinación de los dos insumos que sumen 100 g. En este caso podemos describir la tecnología precisamente por la función de producción:

F (z1, z2 ) = z1 + z2.

De manera más general, cualquier función de producción de la forma

F (z1, z2) = az1 + bz2

Para algunos números no negativos, en a y b las entradas son sustitutos perfectos. Tal función de producción modela una tecnología en la que se puede producir una unidad de producto a partir de 1/a unidades del insumo 1, o de 1/b unidades del insumo 2, o de cualquier combinación de z1 y z2 para las cuales az1 + bz2 = 1. Es decir, una entrada se puede sustituir por la otra a una tasa constante.

Una función de producción que modela una sustitución suave pero no perfecta entre entradas

Muchas tecnologías permiten que los insumos se sustituyan entre sí, pero no a un ritmo constante. Supón que una persona que opera una máquina durante una hora puede producir 100 unidades de producción utilizando 100 unidades de materia prima.

Quizás si se aumenta la velocidad de la máquina, se pueden producir las mismas 100 unidades de producción en 45 minutos utilizando 150 unidades de materia prima, siendo necesaria más materia prima ya que ahora se desperdicia parte.

Pero si la velocidad aumenta nuevamente, reduciendo la cantidad de tiempo de trabajo necesario a 30 minutos, la cantidad de materia prima necesaria puede aumentar en mucho más de 50 unidades, ya que el desperdicio puede aumentar considerablemente.

Una clase de funciones de producción que modela situaciones en las que los insumos pueden sustituirse entre sí para producir el mismo producto, pero no pueden sustituirse a una tasa constante, contiene funciones de la forma

F (z1, z2) = Az1 u z2

Para algunas constantes A, U y V. Esta función de producción se conoce como función de producción Cobb-Douglas.

Un ejemplo de tal función es:

F (z1, z2) = z1 ½ z 2 1/2

Pensamientos finales

La idea misma de una "función de producción" implica la asombrosa analogía del sujeto (la fabricación de cosas, sobre las cuales es apropiado pensar en términos de ingenio, disciplina y planificación) con el modificador (una función matemática, sobre la cual es apropiado pensar en términos de altura, forma y valor único.

2si = dlnQ / dln Fi

Donde Fi es el factor en cuestión. Solow ha señalado de manera perspicaz y provocativa: "La idea de crecimiento endógeno captura tanto la imaginación que los teóricos del crecimiento simplemente insertan suposiciones favorables de una manera inmerecida; y luego, cuando ponen el pulgar y sacan una ciruela que han insertado, hay una tendencia pensar que algo ha sido probado".

Echa un vistazo a: Mapeo De Procesos. Tipos De Mapas, Símbolos, Beneficios Y Más

A juicio de Solow, "probablemente exista un elemento irreductiblemente exógeno en el proceso de investigación y desarrollo, al menos exógeno a la economía". La innovación, aunque puede ser fomentada o inhibida por la existencia de ciertos entornos institucionales, no puede "explicarse" de la misma manera que las leyes físicas y los resultados. En este sentido es exógena o, como preferimos decir, autónoma. Esto no pretende subvalorar de ninguna manera la importancia del cambio de enfoque que ha ocasionado la nueva economía del crecimiento.